Расчёт плоской статически неопределимой рамы методом сил. Расчёт плоской статически неопределимой рамы методом перемещений, страница 9

Знак « – » указывает на то, что поворот сечения L происходит в направлении, противоположном моменту М₁ = 1.

10.2. Определение вертикального линейного перемещения D_2F

 

K

                                                                         а)

 

Эпюра

1,5

                                                                         б)

Рис. 17

Если использовать  вспомогательную систему по рис. 16, а, то эпюра  получится более слож-ной – с тремя участками (LC, CG и GK), что менее выгодно.

Вычисляем D_2F  «перемножением» эпюр (см. рис. 17, б) и М (см. рис. 8) по формуле Симпсона:

 

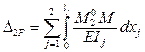
Знак « + » результата говорит о том, что вертикальное перемещение точки K направлено в ту же сторону, что и сила F₂ = 1, т. е.  вниз.  

В заключение заметим, что для определения обоих переме-щений в рассматриваемой раме можно было бы использовать одну и ту же вспомогательную статически определимую систему, причём ту, которая была принята в качестве основной системы  в расчёте рамы  методом сил на действие заданной нагрузки. Эпюры и  в ней – такие же, как на рис. 16, б и 17, б.

11. Расчёт рамы методом сил в матричной форме

Система канонических уравнений метода сил

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

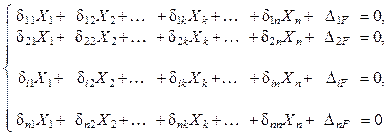                (1.14)

может быть представлена в матричной форме:

. . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . .

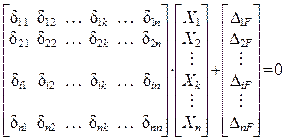   или  (1.15)

                   d                     X         D_F

где d – матрица внешней упругой податливости  основной системы метода сил по направлениям основных неизвестных Х

(или,   что  то  же  самое,  –  по  направлениям  удалённых лишних связей);

Х – вектор*⁾ основных неизвестных;

D_F – вектор*⁾ перемещений в ОСМС по направлениям  удалённых лишних связей от заданной нагрузки.

Матричная формула для определения i-го компонента вектора D_F , основанная на применении формулы Симпсона вычисления интеграла Максвелла – Мора, имеет следующий вид:

D_iF = L_F ,                               (1.16)

где L_i – вектор внутренних усилий в расчётных сечениях элементов  основной системы  в  i-м  единичном  состоянии  (от

X_i  = 1); – транспонированный вектор L_i ;

L_F – вектор внутренних усилий в расчётных сечениях элементов основной системы от заданной нагрузки;

В – квадратная  матрица  внутренней  упругой  податливости основной системы.

*⁾ При расчёте на несколько (n_V) вариантов заданных нагрузок Х и D_F  –

матрицы, имеющие n_V столбцов.

В системах с только изгибаемыми стержнями (балках, рамах без затяжек и т.п. элементов) векторы L_i и L_F  формируются из ординат i-й единичной и грузовой эпюр изгибающих моментов. Матрица B – блочная квазидиагональная, состоящая из матриц податливости расчётных участков основной системы:

B = diag [ B₁ B₂ … B_j … B_m ] (здесь m – число участков).  (1.17)

Структура матрицы B_j податливости j-го участка зависит от того, есть ли на участке распределённая нагрузка или она отсутствует:

– для незагруженного участка  B_j = ;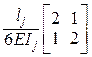

– для участка с распределённой нагрузкой  B_j = .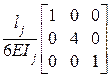

Вектор свободных членов канонических уравнений (грузовых перемещений в ОСМС) вычисляется по матричной формуле

D_F = L_F ,                               (1.18)

где L – матрица усилий  в единичных состояниях ОСМС,  столбцы  которой – векторы усилий в 1-м, 2-м, …, n-м единичных состояниях (от Х₁ = 1,  Х₂ = 1, …, Х_n = 1).

Частным случаем формулы (1.16) является матричное выражение для единичного перемещения:   

d_ik = L_k ,                               (1.19)

а матрица внешней упругой податливости (коэффициентов канонических уравнений) вычисляется как