Реакции связей в единичных и грузовом состояниях основной системы метода
перемещений (ОСМП) можно определять статическим методом – из условия равновесия
узлов и частей ОСМП, а единичные реакции – также и кинематическим методом по формуле*)
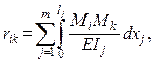 (2.3)
(2.3)
где
rik – реакция i-й введённой связи в
ОСМП от единичного смещения k-й связи (от Zk = 1);
Mi = Mi(xj),
Mk = Mk (xj), EIj
= const;
m – число расчётных участков единичных
эпюр изгибающих моментов Mi и Mk .
*) Для систем с преобладающим
изгибом элементов (рам, балок).
4. Построение эпюр изгибающих моментов
в основной системе
4.1. Эпюры в единичных состояниях ОСМП
Для определения изгибающих моментов от
единичных сме-щений введённых связей предварительно вычисляем погонные изгибные
жёсткости элементов ОСМП: ij = EIj / lj ( j – номер стержня). С учётом того, что, по условиям задачи, EI2 = (4/3)EI1 ,
получаем: i1 = EI1 / l1 = EI1 /(3 м); i2 = EI2 / l2 = (4/3)EI1 /(8 м) = = EI1 /(6 м); i3 = EI3 / l3 = (4/3)EI1 /(4 м) = EI1 /(3 м); i4 = i1; i5 = i2 . Приняв i0 = ij, min = i2 = EI1
/(6 м), имеем i1 = i3
= i4 = 2i0 , i2 = i5
= i0 .
поворота концевых сечений e1 , b2 и b3 элементов 1, 2 и 3, примыкающих к
узлу 1, который поворачивается как бесконечно малый абсолютно жёсткий
Т-образный фрагмент. Следует так-же обеспечить со-блюдение кинема-тических граничныхусловий (в местах опорных закреплений).
С помощью таб-лицы 1 метода
пе-ремещений (При-ложение) строится эпюра изгиба-ющих моментов М1 (рис. 22,
б).
|
|
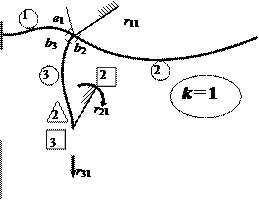
Задаём равное единице смещение первой (
k =
1)
введённой связи – угол поворота
Z1 =
1 – и представляем вызванное им деформированное состояние основной системы (рис. 22, а). При
этом должно быть выполнено
условие совместности
перемещений / деформаций стержней, проявляющееся в равенстве углов
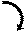


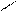














а)



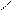
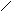
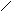


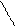
б)
Для каждого прямолинейного участка эпюры М1 вычисляем
соответствующие поперечные силы Qj,1 , используя зависимость Qj,1 = dMj,1 / dxj (
j – номер участка): Q1,1 = (– 8i0 – 4i0 ) / (3
м) = – 4i0 ; Q2,1 =
(0 – 3i0 )/ (8 м) =
– (3/8)i0 ; Q3,1 = (– 8i0 – 4i0 ) /
(4 м) = –
3i0 ; Q4,1 = = 0 ; Q5,1 = 0 .
|
|
|
|
|
|
|
|
|
Второе ( k = 2) единичное состо-яние ОСМП соответствует повороту на
Z2 =
1 второй введённой связи (рис. 23, а). При этом деформируются элементы
3, 4 и 5, примыкающие к узлу 2; их концевые сечения e3 , е4
и b5
поворачиваются на один и тот же угол (условие совместности перемещений
/ деформаций).
С помощью таблицы 1 Приложения определяем
изгибающие моменты М2 и соответствующие им
|
|
|
|
 |
|
|
|
|
|
|
|
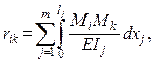 (2.3)
(2.3)![]()
![]()
![]()