СОДЕРЖАНИЕ
ЗАДАЧА № 1. Расчёт
плоской статически неопределимой рамы методом сил ..……………..... 1
ЗАДАЧА
№ 2. Расчёт плоской статически неопределимой рамы методом перемещений ..
32
ПРИЛОЖЕНИЕ. Таблицы метода
перемещений
(стандартные задачи для
типовых элементов основной системы) ………………………………………………………….
61
СПИСОК
ЛИТЕРАТУРЫ …………………………………… 64
ЗАДАЧА № 1
*)
Расчёт плоской статически
неопределимой рамыметодомсил
Основные
положения теории расчёта статически неопределимых систем методом сил студентам
рекомендуется изучать по учебникам [1] (глава 6), [2] (глава 6), [3] (глава 9),
[4] (глава XI), пособию [5] (главы 5 и 9) и разработке
[6] кафедры строительной механики НГАСУ (Сибстрин). Особое внимание при этом
следует уделить выбору основной системы с обязательной проверкой её
геометрической неизменяемости, уяснению смысла канонических уравнений метода
сил и их компонентов (коэффициентов при основных неизвестных и свободных
членов), построению единичных и грузовой эпюр изгибающих моментов с контролем
выполнения условий равновесия, правильному использованию практических способов
вычисления единичных и грузовых перемещений в основной системе (коэффициентов и
свободных членов канонических уравнений) по правилу Верещагина и формуле
Симпсона, проверкам результатов расчёта – статической и, особенно,
кинематической.
З а д а н и е
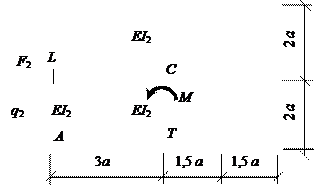
Для рамы, изображённой на рис.
1, требуется:
1. Построить эпюры изгибающих
моментов, поперечных и продольных сил от заданных силовых
воздействий.
 *)
В заданиях к контрольным работам, приведённым в [8], задача числится под номером 7.
*)
В заданиях к контрольным работам, приведённым в [8], задача числится под номером 7.
2. Проверить правильность
построенных эпюр.
3. Определить вертикальное
перемещение точки K и
угол поворота сечения L.
4. Составить матрицы,
необходимые для компьютерно









го
расчёта рамы методом сил
в матричной форме.
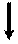
|
|
|
|
|
|
F1 = 20 кН
F2 = 6 кН
q1 = 10
кН/м
q2 = 4 кН/м
М = 24 кН * м
a = 2 м
EI1 : EI2=2 : 1
|
|
|
 |
|
Рис. 1
Р е ш е н
и е
1. Степень
статической неопределимости системы
Степень статической
неопределимости рамы (число лишних связей) можно вычислять по одной из двух
формул:
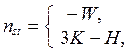 (1.1)
(1.1)
где W = 3D –
2H – C0 (см. тему «Кинематический анализ сооружений»); K – число замкнутых контуров,
образованных элементами системы и диском «земля»; Н – число простых
шарниров.
Если использовать формулу nst = –W, то, считая дисками ломаный стержень ALCGPи стойку TC, имеем D = 2; один простой (не кратный) шарнир С, соединяющий диски друг с
другом (Н = 1); опорных связей в сумме 6 (в
пересчёте на простые линейные связи 1-го типа) – по две в каждом из шарнирных неподвижных
опорных узлов А, Т и Р, т.е. С0 = 6.
Тогда W = 3 * 2 – – 2 * 1 – 6 = –2, nst = –W = 2.
В случае применения формулы nst = 3K – H в рассматриваемой раме можно
обнаружить два замкнутых контура, образованных стержнями системы друг с другом
и диском «земля» – это контуры ALCTA и TCGPT, значит, K = 2. Простых
(не кратных) шарниров – 4 (А, Т, С, Р), т.е. Н
= 4. Следовательно, nst = = 3* 2 – 4 = 2
– конечно, получен тот же результат, что и в первом варианте.
2. Выбор
основной системы
Основную систему метода сил
получаем, удаляя из за-данной рамы две лишние связи (число удаляемых связей n, как правило, принимается равным степени
статической неопределимости рассчитываемой системы: 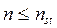 ); взамен
удалённых связей прикладываются их реакции Х1 и Х2,
являющиеся основными неизвестными в расчёте статически неопределимой системы
(СНС) методом сил.
); взамен
удалённых связей прикладываются их реакции Х1 и Х2,
являющиеся основными неизвестными в расчёте статически неопределимой системы
(СНС) методом сил.
Для заданной СНС могут быть
предложены различные варианты основной системы метода сил (ОСМС), из которых выбирают
рациональный, руководствуясь в первую очередь соображениями простоты построения
эпюр (с этой точки зрения, как правило, выгодна ОСМС, имеющая главные и второстепенные
части). Единственное обязательное требование к основной системе – её
геометрическая неизменяемость.






























































![]() *)
В заданиях к контрольным работам, приведённым в [8], задача числится под номером 7.
*)
В заданиях к контрольным работам, приведённым в [8], задача числится под номером 7.
 го
го

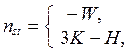 (1.1)
(1.1)![]() ); взамен
удалённых связей прикладываются их реакции Х1 и Х2,
являющиеся основными неизвестными в расчёте статически неопределимой системы
(СНС) методом сил.
); взамен
удалённых связей прикладываются их реакции Х1 и Х2,
являющиеся основными неизвестными в расчёте статически неопределимой системы
(СНС) методом сил.






