







далее на схемах как 1 и 2 . Оба уз







ла – жёсткие, поэтому
nq = 2. Вспомо- б)

гательная шарнирная система изобра-

 жена на рис. 20, а. Она имеет одну сте
жена на рис. 20, а. Она имеет одну сте

 пень свободы – для превращения её в геометрически
неизменяемую требу- Рис. 20
пень свободы – для превращения её в геометрически
неизменяемую требу- Рис. 20
 *) За расчётные узлы принимаются: а) места соединения двух и
более стержней; б) места изменения
жёсткостей сечений элементов; в) опорные узлы с неизвестными
компонентами перемещений. ется
наложить на один из расчётных узлов одну линейную связь (рис. 20, б).
Следовательно, nD =
nл.с.= 1, и рама трижды
кинемати-чески неопределима ( nk
= nq +
nD =
2 + 1 = 3). За основные неизве-стные принимаются углы поворота двух жёстких узлов 1 и
2 (обозначаем их Z1 и Z2 ) и вертикальное линейное перемещение Z3 узла 2.
*) За расчётные узлы принимаются: а) места соединения двух и
более стержней; б) места изменения
жёсткостей сечений элементов; в) опорные узлы с неизвестными
компонентами перемещений. ется
наложить на один из расчётных узлов одну линейную связь (рис. 20, б).
Следовательно, nD =
nл.с.= 1, и рама трижды
кинемати-чески неопределима ( nk
= nq +
nD =
2 + 1 = 3). За основные неизве-стные принимаются углы поворота двух жёстких узлов 1 и
2 (обозначаем их Z1 и Z2 ) и вертикальное линейное перемещение Z3 узла 2.
2. Формирование основной системы
Основную систему получаем наложением
на жёсткие узлы 1 и 2 угловых связей (подвижных защемлений*) ) под номерами



1 и 2 , а также
вертикальной (по направлению основного неизвестного
Z3) линейной связи под
номером 3 на узел 2 (рис.
21).

















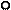

Рис. 21
Для основных неизвестных
приняты следующие правила знаков:
–
положительные углы поворота Z1 и Z2 – по ходу часовой стрелки;
–
положительное линейное перемещение Z3 – вниз.
Замечание:
приведённые правила знаков не являются обяза-тельными, но принятые в начале должны сохраняться до конца расчёта.
Цифрами в кружках на рис. 21
даны
номера
стержневых эле-ментов основной системы, а буквами bj и ej ( j = 1, …,
5) обозначе *)
Используется также термин «плавающая заделка». ны
их концевые сечения ( правило: для
элемента с неодинаковыми закреплениями концов – шарниром на одном конце и защемлением
на другом – началом bjобязательно
назначается защемлённый конец стержня).
*)
Используется также термин «плавающая заделка». ны
их концевые сечения ( правило: для
элемента с неодинаковыми закреплениями концов – шарниром на одном конце и защемлением
на другом – началом bjобязательно
назначается защемлённый конец стержня).
3. Канонические уравнения
Канонические уравнения метода перемещений (КУМП), предназначенные для
определения основных неизвестных Z1 , Z2 и Z3 – перемещений расчётных
узлов, получаются из статических условий R1 = 0, R2 = 0 и R3 = 0 – отрицания реакций дополнительных
связей, введённых в расчётные узлы, от совместного действия на основную систему
заданных нагрузок и смещений введённых связей Z1 , Z2 и Z3 . Расписывая реакции Ri ( i
= 1, 2, 3 ) на основании принципа суперпозиции в
виде Ri = RiZ
+ RiF , полу-чаем уравнения
для определения Z1 … Z3 в каноническом виде:
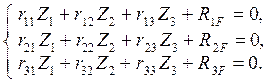 (2.2)
(2.2)
Коэффициенты rik ( i,
k =
1, 2, 3 ) при неизвестных Z1 , Z2 и Z3 и свободные члены RiF ( i
= 1, 2, 3 ) канонических уравнений – реакции введённых связей от
единичных основных неизвестных Z1 = 1, Z2 = 1, Z3 = 1 ( в
отдельности ) и от заданной нагрузки.
![]()
![]()
![]() жена на рис. 20, а. Она имеет одну сте
жена на рис. 20, а. Она имеет одну сте![]()
![]()
![]() пень свободы – для превращения её в геометрически
неизменяемую требу- Рис. 20
пень свободы – для превращения её в геометрически
неизменяемую требу- Рис. 20 ![]() *) За расчётные узлы принимаются: а) места соединения двух и
более стержней; б) места изменения
жёсткостей сечений элементов; в) опорные узлы с неизвестными
компонентами перемещений. ется
наложить на один из расчётных узлов одну линейную связь (рис. 20, б).
Следовательно, nD =
nл.с.= 1, и рама трижды
кинемати-чески неопределима ( nk
= nq +
nD =
2 + 1 = 3). За основные неизве-стные принимаются углы поворота двух жёстких узлов 1 и
2 (обозначаем их Z1 и Z2 ) и вертикальное линейное перемещение Z3 узла 2.
*) За расчётные узлы принимаются: а) места соединения двух и
более стержней; б) места изменения
жёсткостей сечений элементов; в) опорные узлы с неизвестными
компонентами перемещений. ется
наложить на один из расчётных узлов одну линейную связь (рис. 20, б).
Следовательно, nD =
nл.с.= 1, и рама трижды
кинемати-чески неопределима ( nk
= nq +
nD =
2 + 1 = 3). За основные неизве-стные принимаются углы поворота двух жёстких узлов 1 и
2 (обозначаем их Z1 и Z2 ) и вертикальное линейное перемещение Z3 узла 2. 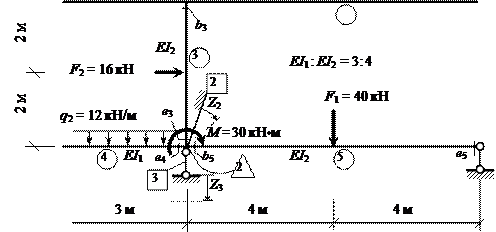
![]() *)
Используется также термин «плавающая заделка». ны
их концевые сечения ( правило: для
элемента с неодинаковыми закреплениями концов – шарниром на одном конце и защемлением
на другом – началом bjобязательно
назначается защемлённый конец стержня).
*)
Используется также термин «плавающая заделка». ны
их концевые сечения ( правило: для
элемента с неодинаковыми закреплениями концов – шарниром на одном конце и защемлением
на другом – началом bjобязательно
назначается защемлённый конец стержня).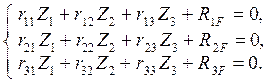 (2.2)
(2.2)