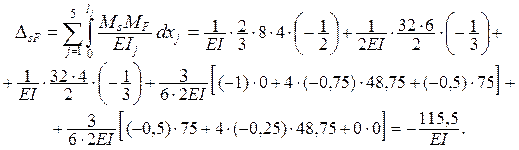
Подсчитываем сумму всех коэффициентов канонических уравнений:
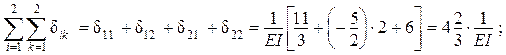 полученный результат совпадает с dss , что свидетельствует о правильности определения коэффициентов dik (i, k = 1, 2) .
полученный результат совпадает с dss , что свидетельствует о правильности определения коэффициентов dik (i, k = 1, 2) .
Сумма свободных членов равнений:
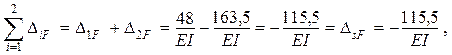
следовательно,
перемещения DiF (i
= 1, 2) вычислены верно.
7. Определение основных неизвестных
Подставляем найденные значения коэффициентов и свободных членов в канонические
уравнения метода сил (1.2):
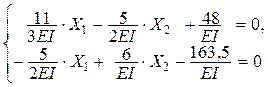
или,
после умножения на EI:
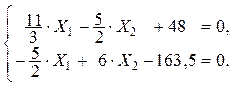
Решив систему уравнений, получаем Х1 = 7,667 кН * м ;
Х2 = 30,444
кН * м.
При решении системы «вручную» имеет смысл
проверить найденные значения Х1 и Х2 их подстановкой
в уравнения.
8. Определение внутренних усилий в заданной раме
и построение их эпюр
Начинаем с вычисления
изгибающих моментов. На основании принципа независимости (суперпозиции) воздействий:
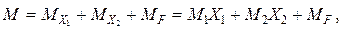 (1.9)
(1.9)
где два первых слагаемых – это
изгибающие моменты в основной системе от реакций Х1 и Х2 удалённых лишних связей, а MF – моменты от заданной нагрузки.

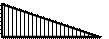
Эпюры
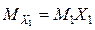
и
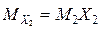
приведены на рис.
8, а, б, эпюра
MF – на рис. 6. Эпюра искомых моментов
в раме представлена на рис. 8, в.
Эпюра 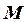
(кН * м)
|
|



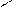
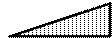 а) б)
а) б)
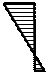
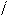
 в)
в)
Рис. 8
По найденным изгибающим моментам М определяем поперечные силы Q,
используя дифференциальную зависимость
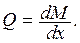 (1.10)
(1.10)
На прямолинейных участках эпюры М (где отсутствует рас-пределённая
нагрузка) Q вычисляется как тангенс угла наклона эпюры
М к её оси – отношение приращения DM (разности
значений моментов по концам участка) к длине участка. Для горизонтальных
участков DM вычисляется
как разность моментов на правом и левом концах, а для вертикальных – верхнем и нижнем.
Так, на участке LС: 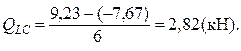 Аналогично
Аналогично
Поперечные силы в
концевых сечениях участка GP определяются
из условий равновесия стержня (рис. 9):
SmG = 0: 30,44 – q1 * 6 * 3 –
– F1 * 3 – QPG * 6 = 0,
QPG = – 34,93 кН;
|
|
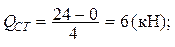
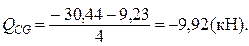
Рис. 9
 Sy = 0: QG P – q1 * 6 – F1 – QPG = 0 QG P = 45,07 кН.
Sy = 0: QG P – q1 * 6 – F1 – QPG = 0 QG P = 45,07 кН.
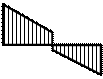
Эпюра Q на участке
GP строится обычным порядком; в месте
приложения нагрузки F1 – скачок
на величину силы.
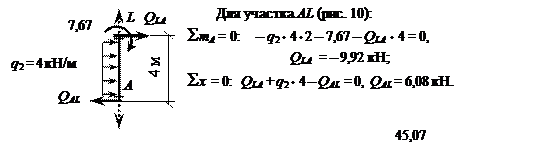
Эпюра 
(кН)
|
|

Рис. 10
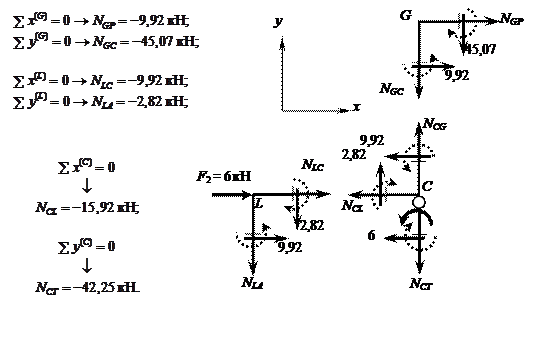
Рис. 12
Эпюра 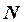
(кН)
|
|





Эпюра продольных сил в стержнях рамы – на рис.
13.
Рис. 13
9. Проверки результатов расчёта
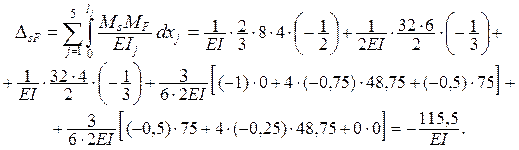
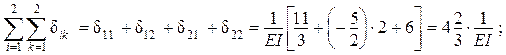 полученный результат совпадает с dss , что свидетельствует о правильности определения коэффициентов dik (i, k = 1, 2) .
полученный результат совпадает с dss , что свидетельствует о правильности определения коэффициентов dik (i, k = 1, 2) .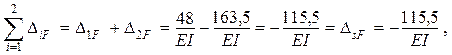
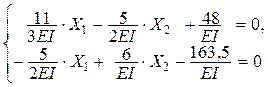
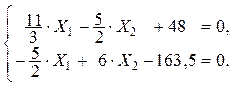
![]() (1.9)
(1.9)


![]()
![]() а) б)
а) б)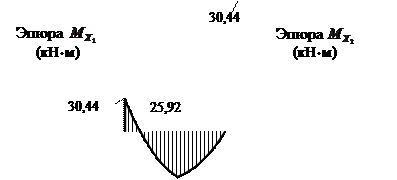
![]()
![]()
![]()
![]()
![]() в)
в)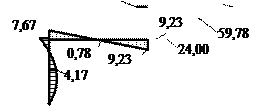
![]() (1.10)
(1.10)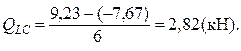 Аналогично
Аналогично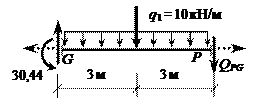
![]() Sy = 0: QG P – q1 * 6 – F1 – QPG = 0 QG P = 45,07 кН.
Sy = 0: QG P – q1 * 6 – F1 – QPG = 0 QG P = 45,07 кН.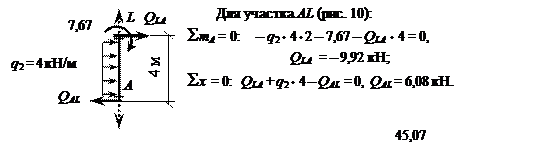


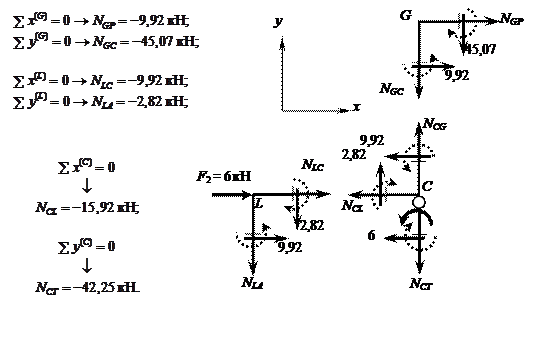

 Эпюра продольных сил в стержнях рамы – на рис.
13.
Эпюра продольных сил в стержнях рамы – на рис.
13.