Заключение: значения усилий и
перемещений, полученные в результате компьютерного расчёта, практически совпадают
с вычисленными ранее «вручную». Расхождения в 4-й значащей цифре объясняются
округлениями компонентов матрицы податливости В.
ЗАДАЧА № 2
*)
Расчёт плоской статически
неопределимой рамыметодомПЕРЕМЕЩЕНИЙ
Основные
положения теории расчёта статически неопределимых систем методом перемещений
студентам рекомендуется изучать по учебникам [1] (глава 7), [2] (глава 7), [3]
(глава 10), [4] (глава XII),
пособию [5] (глава 7) и разработке [7] кафедры строительной механики НГАСУ
(Сибстрин). К принципиально важным вопросам, требующим особого внимания, относятся:
определение числа основных неизвестных (степени кинематической
неопределимости), формирование основной системы, уяснение смысла канонических
уравнений метода сил и их компонентов (коэффициентов при основных неизвестных и
свободных членов), правильное представление и изображение деформированных
состояний основной системы от единичных смещений введённых связей и от заданной
нагрузки, построение эпюр изгибающих моментов в единичных и грузовом состояниях
с помощью таблиц стандартных задач метода перемещений, способы определения
коэффициентов и свободных членов канонических уравнений, проверки результатов
расчёта.
F1 = 40 кН
F2 = 16
кН
q1 = 5
кН/м
q2 = 12
кН/м
М = 30
кН * м
l1 = 3 м
l2 = 8 м
h
= 4 м
EI1 : EI2=3 :
4
|
|
З а д а н и е
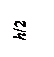
Рис. 19
Для рамы, изображённой на рис. 19, требуется:
1. Построить эпюры изгибающих моментов, поперечных и продольных сил.
*)
В заданиях к контрольным работам, приведённым в [8], задача числится под номером 9.
2. Проверить правильность построенных эпюр.
3. Составить матрицы, необходимые для компьютерного расчёта рамы.
Р е ш е н и е
1. Степень кинематической неопределимости системы
За основные неизвестные в расчёте по методу перемещений принимаются независимые
угловые и линейные перемещения расчётных узлов *). Число
основных неизвестных называется степенью кинематической неопределимости
системы и вычисляется по формуле
nk = nq + nD ,
(2.1)
где nq – степень угловой подвижности узлов – число неизвестных углов поворота жёстких внутренних (неопорных)
узлов, равное числу таких
узлов плоской системы;
nD – степень линейной
подвижности узлов – число независимых неизвестных линейных
перемещений всех узлов системы, включая опорные.
Для определения
nD можно использовать вспомогательную
шарнирную
систему, получаемую из заданной рамы введением цилиндрических шарниров во
все жёсткие узлы – внутренние и опорные. С её помощью степень подвижности
nD находится как
число степеней свободы шарнирной
системы
Wш.с. или, что то же самое, как число
nл.с. внешних линейных
связей, которые нужно наложить на узлы шарнирной системы для обеспечения её геометрической
неизменяемости.
В рассматриваемой раме (рис. 20) а)
расчётными являются узлы
B
и
G (по
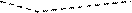
признакам «а» и «б»),
обозначаемые
