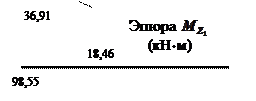ОСМП, должен
быть равен сумме всех коэффи-циентов канонических уравнений
Суммарное
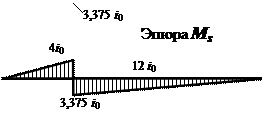
еди-ничное состояние ос-новной системы показано на рис. 30, а, а суммарная единичная
эпюра изгибающих моментов Ms –
на
рис. 30, б.
|
|

моменты в





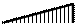 б)
б)
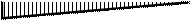


Рис. 30
Используя правило Верещагина для «умножения» эпюры Msсамой на
себя, находим rss по формуле (2.4), учитывая при этом антисимметрию
эпюры относительно горизонтальной оси, что позволяет выполнить вычисления для
половины системы с последующим удвоением:
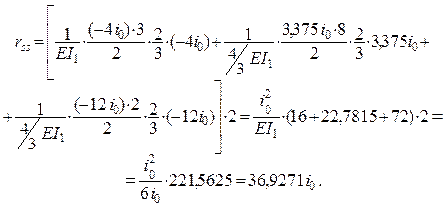
Полученный результат сравниваем с суммой коэффициентов
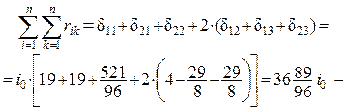
rss и  совпадают в шести значащих цифрах, что свидетельствует
о правильности вычисления коэффициентов канонических уравнений.
совпадают в шести значащих цифрах, что свидетельствует
о правильности вычисления коэффициентов канонических уравнений.
О способе проверки свободных членов уравнений «перемножением» эпюр можно узнать
из [7]. Здесь эту проверку не выполняем.
7. Определение основных неизвестных
Подставляем найденные значения
коэффициентов и свободных членов в канонические уравнения метода перемещений
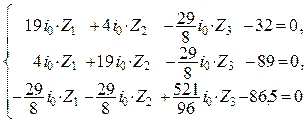
или,
после деления на i0:
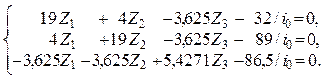
Решив систему уравнений, находим основные неизвестные:
Z1 = 4,6135
/ i0 ; Z2 = 8,4131 /
i0 ; Z3 = 24,6378 /
i0 .
Следует заметить, что все перемещения узлов обратно пропорциональны параметру
жёсткости i0 . Знаки
«+» указывают на то, что направления перемещений – такие, как на рис. 21: повороты
обоих расчётных узлов происходят по ходу часовой стрелки, а вертикальное
линейное перемещение – вниз.
Правильность решения системы уравнений контролируется подстановкой в них
найденных значений Z1 , Z2 и Z3 – невязка не превышает
0,01 % .
8. Определение внутренних усилий в заданной раме
и построение их эпюр. Проверка результатов расчёта
В первую очередь вычисляем изгибающие моменты. Согласно принципу независимости
(суперпозиции) воздействий:
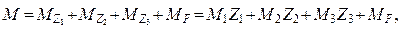 (2.5)
(2.5)
Эпюры 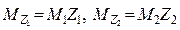 и и 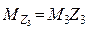 приведены на рис. 31, а, б, в; эпюра MF – на рис. 25, б. приведены на рис. 31, а, б, в; эпюра MF – на рис. 25, б.
Эпюра искомых моментов М в раме представлена
на рис. 32.
|
|
где три первых слагаемых – это изгибающие
моменты в основной системе от перемещений
Z1 ,
Z2 и
Z3 расчётных узлов, а
MF – моменты от
заданной нагрузки.


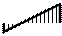
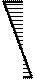
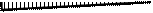
а)


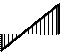

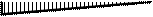


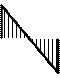
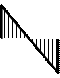


Эпюра 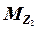
(кН * м)
|
|
Эпюра 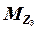
(кН * м)
|
|
б)
в)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() б)
б) 
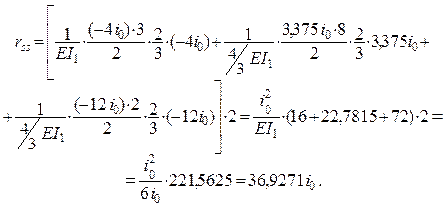
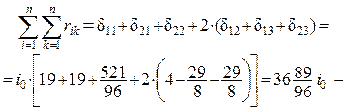
 совпадают в шести значащих цифрах, что свидетельствует
о правильности вычисления коэффициентов канонических уравнений.
совпадают в шести значащих цифрах, что свидетельствует
о правильности вычисления коэффициентов канонических уравнений. 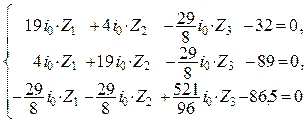
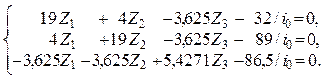
![]() (2.5)
(2.5)![]()
![]()