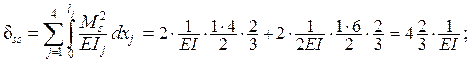Вычисляем коэффициенты
канонических уравнений – единичные перемещения, учитывая заданное соотношение
изгибных жёсткостей сечений горизонтальных и вертикальных стер-жней EI1 : EI2=2 : 1. Обозначив
для краткости EI2= EI ,
имеем EI1= 2EI.
Главные коэффициенты
– собственные перемещения d
11 и
d
22 – находим «перемножением» каждой из эпюр
М1
и
М2 самой на себя. При этом учитываем, что эпюра
М1
имеет два одинаковых по длинам и абсолютным значениям ординат треугольных участка
на вертикальных стержнях и два – на горизонтальном, а эпюра
М2
– на горизонтальных. Используем правило Верещагина (1.5):
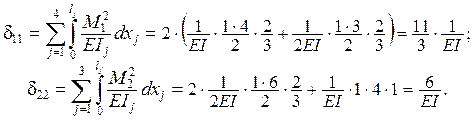
Побочные коэффициенты d12 и d21 находим «перемножением» единичных эпюр М1
и М2 , принимая во внимание равенство d12 и d21 по теореме Максвелла о взаимности единичных перемещений.
Интеграл в формуле Максвелла – Мора на нижнем горизонтальном
участке вычисляем по формуле Симпсона (1.6), а на верхнем вертикальном – по
правилу Верещагина. На остальных участках результат интегрирования – заведомо
нулевой, так как по всей длине этих участков либо М1 = 0,
либо М2 = 0.
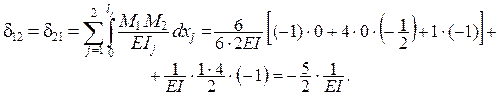
Свободные члены канонических уравнений – грузовые
перемещения D1F и D2F – определяем
«перемножением» эпюры MF с
единичными эпюрами М1 и М2 . Для
вычисления интегралов в выражениях D1F и D2F на двух грузовых участках эпюры
MF верхнего горизонтального стержня используем формулу
Симпсона, а на всех остальных участках – правило Верещагина.
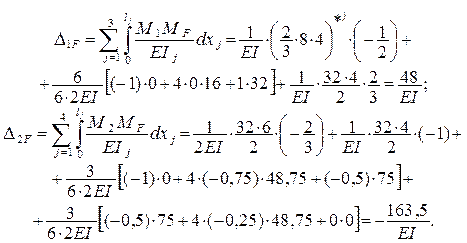
6. Проверка правильности определения коэффициентов
и свободных членов канонических уравнений
Для проверки используется эпюра суммарных единичных моментов Ms ,
получаемых от одновременного действия всех основных неизвестных, равных единице (
Xk = 1, k = 1, 2, …, n ). При
отсутствии ошибок в вычислении коэффициентов и свободных членов должны
выполняться равенства
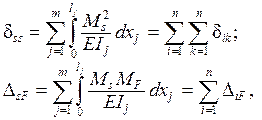
где
dss и DsF– обобщённые
перемещения, представляющие собой суммы перемещений в основной системе по направлениям удалённых связей соответственно от одновременного действия всех основных неизвестных
Х1 = 1, Х2 = 1, …, Хn = 1 и от нагрузки.


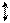







*
) Площадь параболического сегмента:
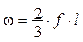
.
f
Строим эпюру Ms , рассчитывая основную систему на совместное действие
Х1 = 1 и Х2 = 1*) (рис. 7).
Опорные реакции в суммарном единичном
состоянии:
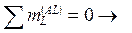 НА,s = 1/(4 м);
НА,s = 1/(4 м); 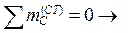 НТ,s = 0;
НТ,s = 0;
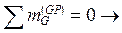 VP,s = –1/(6 м);
VP,s = –1/(6 м);
S x
= 0 для всей рамы 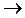 НР,s = НА,s = 1/(4 м);
НР,s = НА,s = 1/(4 м);
S mG = 0  VA,s = (HA,s * 8 м + VP,s
* 4 м) / 6
м = 1/(6 м);
VA,s = (HA,s * 8 м + VP,s
* 4 м) / 6
м = 1/(6 м);
S y = 0
 VT,s
VT,s = –
VA,s –
VP,s
= 0.
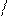
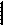


















а) б)




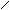


Рис. 7
Для контроля суммируем эпюры М1
и М2 – получается тот же результат – эпюра Ms , что служит дополнительным свидетельством правильности построения всех
единичных эпюр – М1 , М2 и Ms .
Вычисляем обобщённые перемещения dss и DsF :
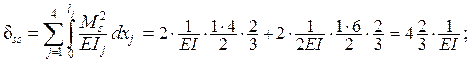
*)
Не следует получать эпюру Ms суммированием единичных эпюр Mi , так как при этом в неё могут быть перенесены ошибки, не обнаруженные в эпюрах Mi .
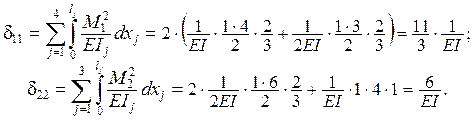
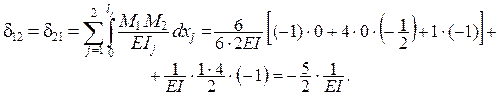
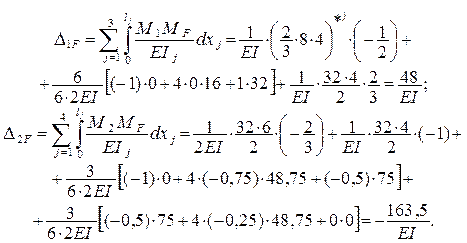
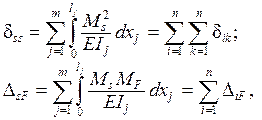
![]() НА,s = 1/(4 м);
НА,s = 1/(4 м); ![]() НТ,s = 0;
НТ,s = 0; ![]() VP,s = –1/(6 м);
VP,s = –1/(6 м); ![]() НР,s = НА,s = 1/(4 м);
НР,s = НА,s = 1/(4 м); ![]() VA,s = (HA,s * 8 м + VP,s
* 4 м) / 6
м = 1/(6 м);
VA,s = (HA,s * 8 м + VP,s
* 4 м) / 6
м = 1/(6 м); ![]()
![]()
![]()
![]()

 а) б)
а) б)

![]()
![]()
![]()
![]()