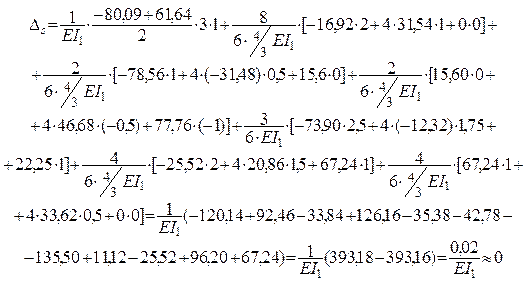Сущность проверки состоит в вычислении
перемещений в статически определимой основной системе метода сил, полученной
из заданной системы удалением лишних связей, по направлениям этих связей. Если
приложить к основной системе заданную нагрузку и реакции лишних связей (взяв их
как соответствующие силовые факторы из результатов расчёта методом перемещений),
то при отсутствии ошибок в этих результатах усилия в основной системе метода
сил и деформации её элементов, а следовательно, и перемещения в ней совпадут с
усилиями, деформациями и перемещениями в заданной статически неопределимой
системе. При этом перемещения по направлениям удалённых лишних связей заведомо
равны нулю, если удалённые связи – абсолютно жёсткие.
При выполнении кинематической проверки вычисляется обобщённое перемещение Ds – сумма
перемещений по направлениям всех удалённых лишних связей:
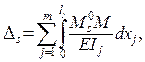 (2.6)
(2.6)
где 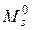 – суммарные единичные изгибающие
моменты (от одновременного действия на основную систему метода сил единичных реакций всех удалённых лишних связей
– суммарные единичные изгибающие
моменты (от одновременного действия на основную систему метода сил единичных реакций всех удалённых лишних связей
Х1 =
1, Х2 = 1, …, Хn = 1);
М – изгибающие моменты в заданной статически неопределимой системе, найденные
расчётом рамы методом перемещений (рис. 32).
Для выбора вспомогательной
основной системы метода сил
 выявляем степень статической
выявляем степень статической


 неопределимости рассчитыва
неопределимости рассчитыва емой рамы, используя формулу
емой рамы, используя формулу

 nst
nst = 3
K –
H, (2.7)

 где K – число
замкнутых конту
где K – число
замкнутых конту





ров, образованных эле
ментами системы и диском «земля»;
Н – число
простых шарниров. Рис. 40
Для заданной рамы K =
3, H =
4 (рис. 40), тогда nst =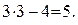
Выбираем основную систему метода сил (с
обязательной проверкой её неизменяемости) и прикладываем к ней единичные
реакции удалённых лишних связей (рис. 41, а).








а)
б)











|
|
|
|
|
|
|
 |
|
|
Эпюра 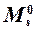
|
|
|
|
|
|
|
 Рис. 41
Рис. 41
Для определения суммарных единичных моментов 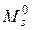 предварительно находим опорные реакции, начиная с любой из
предварительно находим опорные реакции, начиная с любой из
VD , VC или VP: 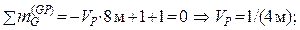 аналогично из
аналогично из 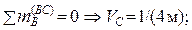
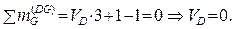 Далее из условия равновесия всей системы
Далее из условия равновесия всей системы
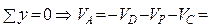
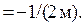 Отделив
верхнюю Т-образную часть DPB,
имеем:
Отделив
верхнюю Т-образную часть DPB,
имеем:
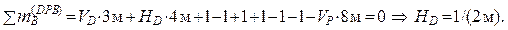
Наконец, для системы в
целом: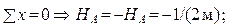
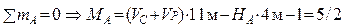 , после
чего строится эпюра
, после
чего строится эпюра 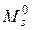 (рис. 41, б). Заметим, что в стержнях DG, GP, GB и BC, имеющих шарниры на обоих концах, моменты могут
быть найдены без использования опорных реак-ций – по легко определяемым
значениям в концевых сечениях.
(рис. 41, б). Заметим, что в стержнях DG, GP, GB и BC, имеющих шарниры на обоих концах, моменты могут
быть найдены без использования опорных реак-ций – по легко определяемым
значениям в концевых сечениях.
Для вычисления Ds по формуле (2.6) «перемножаем» эпюры 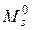 (рис. 41, б) и М (см. рис.
32) – по правилу Верещагина на участке DG и по формуле Симпсона на остальных:
(рис. 41, б) и М (см. рис.
32) – по правилу Верещагина на участке DG и по формуле Симпсона на остальных:
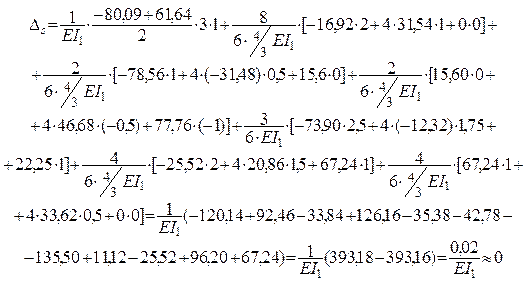
Вывод: результаты статической и
кинематической проверок свидетельствуют о правильности решения задачи и достаточной
точности выполненного расчёта.
9. Расчёт рамы методом перемещений в матричной форме
Система канонических уравнений метода перемещений
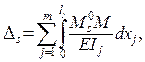 (2.6)
(2.6)![]() – суммарные единичные изгибающие
моменты (от одновременного действия на основную систему метода сил единичных реакций всех удалённых лишних связей
– суммарные единичные изгибающие
моменты (от одновременного действия на основную систему метода сил единичных реакций всех удалённых лишних связей выявляем степень статической
выявляем степень статической![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() неопределимости рассчитыва
неопределимости рассчитыва![]() емой рамы, используя формулу
емой рамы, используя формулу![]()
![]()
![]() где K – число
замкнутых конту
где K – число
замкнутых конту![]()
![]()
![]()
![]()
![]()
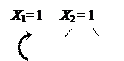
![]()
![]()
![]()
![]()


![]() Рис. 41
Рис. 41![]() предварительно находим опорные реакции, начиная с любой из
предварительно находим опорные реакции, начиная с любой из![]() аналогично из
аналогично из ![]()
![]() Далее из условия равновесия всей системы
Далее из условия равновесия всей системы
![]()
![]() Отделив
верхнюю Т-образную часть DPB,
имеем:
Отделив
верхнюю Т-образную часть DPB,
имеем:![]()
![]()
![]() , после
чего строится эпюра
, после
чего строится эпюра ![]() (рис. 41, б). Заметим, что в стержнях DG, GP, GB и BC, имеющих шарниры на обоих концах, моменты могут
быть найдены без использования опорных реак-ций – по легко определяемым
значениям в концевых сечениях.
(рис. 41, б). Заметим, что в стержнях DG, GP, GB и BC, имеющих шарниры на обоих концах, моменты могут
быть найдены без использования опорных реак-ций – по легко определяемым
значениям в концевых сечениях.![]() (рис. 41, б) и М (см. рис.
32) – по правилу Верещагина на участке DG и по формуле Симпсона на остальных:
(рис. 41, б) и М (см. рис.
32) – по правилу Верещагина на участке DG и по формуле Симпсона на остальных: