d = 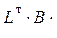 L . (1.20)
L . (1.20)
Решение системы канонических
уравнений (1.15) в матричной форме даёт вектор искомых значений основных
неизвестных:
Х = – d –1 DF , (1.21)
где « – 1 » – символ обращения матрицы.
Подстановка в (1.21) выражений (1.18) и (1.20) приводит к матричной формуле
Х
= – (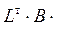 L)–1 (
L)–1 (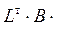 LF ) , (1.22)
LF ) , (1.22)
S = 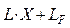 (1.23) (1.23)
|
|
Искомые усилия в расчётных
сечениях заданной СНС определяются как или, с учётом (1.22):
S = LF – 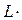 (
(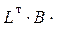 L)–1 (
L)–1 (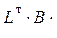 LF ) , (1.24)
LF ) , (1.24)
где
в случае расчёта системы с преобладающим изгибом элементов (балка, рама) под S подразумеваются
изгибающие моменты М. Из (1.24) видно, что для вычисления усилий в рассчитываемой
системе должны быть составлены три исходные матрицы: усилий в ОСМС – единичных L и от заданной нагрузки LF ,
а также матрица внутренней упругой податливости В.
Кинематическая (деформационная) проверка найденных усилий S выполняется
по матричной формуле
D = 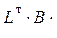 S. (1.25)
S. (1.25)
При отсутствии ошибок в S результатом вычисления D по (1.25) должен быть вектор со всеми нулевыми
компонентами.
Матричная форма расчёта удобна
для компьютерного программирования, с использованием стандартных подпрограмм и
процедур для выполнения предписываемых соотношением (1.24) операций с матрицами
(умножения, транспонирования, обращения и сложения / вычитания). Следует заметить, что современные
компьютеры выполняют вычислительные операции с чрезвычайно высокой точностью,
поэтому проверка по (1.25) при автоматизированном (компьютерном) расчёте теряет
смысл, так как она всегда выполняется, даже если исходные матрицы
содержат ошибки.
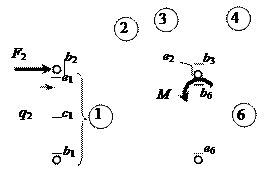
Составим исходные матрицы для
статически неопределимой рамы (см.
рис. 1), расчёт которой в обычной (нематричной) форме выполнен выше. Основная
система рамы имеет 6 расчётных участков (рис. 18) – их границы совпадают с границами
грузовых участков в двух единичных (см. рис. 4 и 5) и грузовом (см. рис. 6) состояниях.
Номера расчётных участков даны на рис. 18 цифрами в кружках.
На участках 2, 3 и 6, где нет
распределённой нагрузки, назначаем по два расчётных сечения – в начале и конце
каждого участка, обозначая их соответственно bj и ej *) (здесь j – номер
 *) От англ. beginning
– начало, end – конец.
*) От англ. beginning
– начало, end – конец.
участка). На 1-м, 4-м и 5-м участках,
где имеются распределённые нагрузки, кроме концевых сечений, назначены также
сечения посредине участков ( cj ).



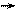


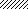



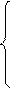


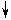
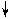




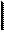
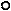
Рис. 18
От Х1 = 1 От Х2 = 1 От нагрузки
Участки
|
|
Структура
столбцов обеих матриц (порядок записи компонентов, вы- ражающих
ординаты эпюр М1
, М2 и МF ) – одинаковая (по участкам с 1-го по 6-й). Матрица L имеет два столб-ца (по
числу единичных состояний основной системы), а LF – один столбец (задан один вариант загружения рамы).
При записи в матрицы положительными
|
|
Формируем матрицы усилий
L
и
LF в расчётных сечениях ОСМС в единичных и грузовом
состояниях. Матрицы имеют одинаковое число строк, равное суммарному количеству
назначенных сечений (всего 15).
![]() L . (1.20)
L . (1.20)![]() L)–1 (
L)–1 (![]() LF ) , (1.22)
LF ) , (1.22)![]() (
(![]() L)–1 (
L)–1 (![]() LF ) , (1.24)
LF ) , (1.24)![]() S. (1.25)
S. (1.25)![]() *) От англ. beginning
– начало, end – конец.
*) От англ. beginning
– начало, end – конец.