Расчёт плоской статически неопределимой рамы методом сил. Расчёт плоской статически неопределимой рамы методом перемещений, страница 4

 

6 м

6 м

1

                                                                                  в)

    

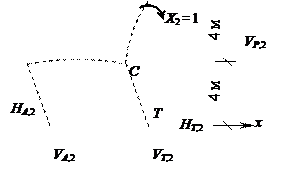
  Рис. 5

Используя для определения опорных реакций те же приёмы, что и в предыдущем случае, находим Н_А,2 = 0, Н_Т,2  = 0, Н_Р,2 = 0, V_P,2  = – 1/(6 м), V_А,2 = – 1/(6 м), V_Т,2 = 1/(3 м). Эпюра изгибающих моментов М₂ представлена на рис. 5, б, а проверка равновесия  узлов – на рис. 5, в. Заметим, что на рис. 4, в  и  5, в не показаны продольные и поперечные силы в сечениях у узлов, так как в силу бесконечной малости их плеч относительно центров узлов они не входят в уравнения равновесия моментов.

 4.2. Эпюра изгибающих моментов в грузовом состоянии ОСМС

y

        Схема основной системы, к которой приложена заданная нагрузка, приведена на рис. 6, а.

 

48,75

G

HP,F

VP,F

                 а)                                                         б)

P

                                                                           

 

3 м

3 м

6 м

24

24

                                                                                          в)

    

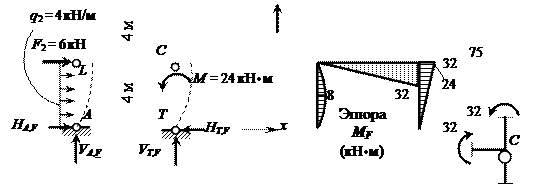
      Рис. 6

Находим опорные реакции (в той же последовательности, что и в единичных состояниях):

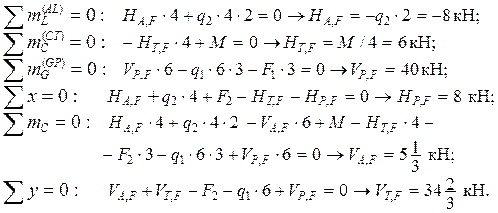
Построив  эпюру  M_F  (рис. 6, б),  для  проверки  вырезаем   узел С (рис. 6, в) – моменты в нем уравновешены.

5. Вычисление коэффициентов и свободных членов

канонических уравнений метода сил

Коэффициенты d_ik и свободные члены D_iF (i, k = 1, 2, …, n) – единичные и грузовые перемещения в ОСМС – определяются методом Максвелла – Мора  по  формулам (1.3а)  и  (1.4).  Входящие в них интегралы можно вычислять, используя правило    Верещагина  или  формулу Симпсона.

Правило Верещагина применимо в случае, когда хотя бы одна из «перемножаемых» эпюр изгибающих моментов – линейная в пределах участка длиной l_j :

интеграл вида 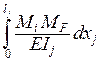 при EI_j = constравен 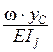,     (1.5)

где w – площадь одной из «перемножаемых» эпюр (криволинейной, ломаной, прямолинейной); у_С – ордината другой (обязательно прямолинейной) эпюры, взятая под центром тяжести первой эпюры. Значения w и у_С  берут с учётом их знаков.

Сложные эпюры следует раскладывать на простые составляющие (прямоугольники, треугольники, параболические сегменты), для каждой из которых известно положение центра тяжести и легко находится площадь w.

Формула Симпсона применяется в пределах грузового участка длиной l_j, где каждая из двух «перемножаемых» функций M_i (в единичном состоянии) и M_F (в грузовом состоянии) имеет единое аналитическое выражение:

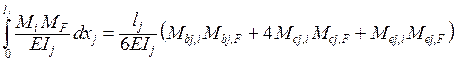,  (1.6)

где M_bj,i , M_cj,i , M_ej,i – изгибающие моменты  в  единичном ( i ) сосостоянии,  действующие  соответственно  в начале  ( в сечении b_j ),  на конце  ( в сечении

e_j )  и посредине ( в сечении c_j ) j-го участка;

M_bj,F , M_cj,F , M_ej,F – изгибающие моменты  в  тех же сечениях  в грузовом ( F ) состоянии;  EI_j = const.

Моменты подставляются в (1.6) с учётом их знаков. Формула Симпсона дает точное значение определённого интеграла, если произведение M_iM_F  является полиномом не выше 3-й степени.

В подынтегральные выражения формул (1.5) и (1.6) вместо M_F  может входить момент M_k  в единичном состоянии.