В системах с преобладающим изгибом (балках и рамах) перемещения от силовых
воздействий с достаточной для практических целей точностью можно определять,
пренебрегая влиянием деформаций сдвига и растяжения - сжатия, по
формуле Максвелла – Мора, в которой удерживается только
один член – содержащий изгибающие моменты:
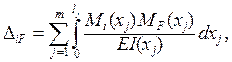 (1.3)
(1.3)
где
m – число расчётных участков эпюр изгибающих моментов –
единичной Mi и грузовой MF .
Формулу (1.3) далее будем записывать в виде
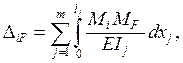 (1.3а
)
(1.3а
)
подразумевая
Mi = Mi(xj), MF = MF (xj), EIj = const.
Формула для определения единичных перемещений dik (коэффициентов канонических уравнений) получается как частный случай
(1.3а), если в качестве силового воздействия, от которого возникает это
перемещение, выступает единичное основное неизвестное Xk = 1:
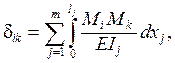 (1.4)
(1.4)
4. Построение эпюр изгибающих моментов
в основной системе
4.1. Эпюры в единичных состояниях ОСМС
Рассматриваем два состояния основной системы – отдельно от действия Х1
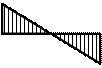
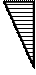
= 1 и Х2 = 1. Первое из них показано на рис. 4, а, где
штриховыми линиями изображены оси деформированных стержней. По схеме деформаций
можно представить геометрический смысл коэффициентов d11 и d21 – это
относительные (вза-имные) углы поворота пар сечений бесконечно близко ниже и
правее шарниров L и G соответственно.
Для определения изгибающих моментов М1 , возникающих от Х1
= 1, предварительно находим реакции опор А, T и Р
в сле














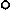




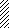
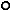


а) б)







в)
Рис. 4
дующем порядке: из условий равновесия стержней AL,
СТ и GP
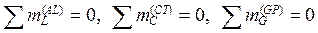 получаем НА,1 =
1/(4 м), НТ,1 = 0 и VP,1 =
0, затем из уравнения S x = 0 для всей рамы
получаем НА,1 =
1/(4 м), НТ,1 = 0 и VP,1 =
0, затем из уравнения S x = 0 для всей рамы  НР,1
= НА,1 = 1/(4 м), из S mG = 0
НР,1
= НА,1 = 1/(4 м), из S mG = 0  VA,1 = HA,1 * 8 м
/(6 м) = 1/(3 м) и, наконец, из уравнения S y
= 0
VA,1 = HA,1 * 8 м
/(6 м) = 1/(3 м) и, наконец, из уравнения S y
= 0  VT,1 = – VA,1 = –1/(2 м). Вычислив изгибающие моменты в характерных сечениях
рамы (у узлов L и С)
и учитывая, что в сечениях у шарниров А, Т, и Р моменты
равны нулю, строим эпюру М1 (рис. 4, б). Для контроля
проверяем равновесие моментов в узлах (рис. 4, в).
VT,1 = – VA,1 = –1/(2 м). Вычислив изгибающие моменты в характерных сечениях
рамы (у узлов L и С)
и учитывая, что в сечениях у шарниров А, Т, и Р моменты
равны нулю, строим эпюру М1 (рис. 4, б). Для контроля
проверяем равновесие моментов в узлах (рис. 4, в).
Второе единичное состояние
основной системы (от действия
Х2 =
1) изображено
на рис. 5, а.


















а) б)
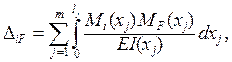 (1.3)
(1.3)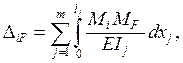 (1.3а
)
(1.3а
)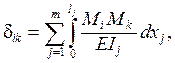 (1.4)
(1.4)




 а) б)
а) б)
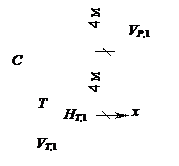
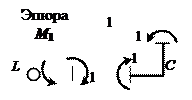
![]() получаем НА,1 =
1/(4 м), НТ,1 = 0 и VP,1 =
0, затем из уравнения S x = 0 для всей рамы
получаем НА,1 =
1/(4 м), НТ,1 = 0 и VP,1 =
0, затем из уравнения S x = 0 для всей рамы ![]() НР,1
= НА,1 = 1/(4 м), из S mG = 0
НР,1
= НА,1 = 1/(4 м), из S mG = 0 ![]() VA,1 = HA,1 * 8 м
/(6 м) = 1/(3 м) и, наконец, из уравнения S y
= 0
VA,1 = HA,1 * 8 м
/(6 м) = 1/(3 м) и, наконец, из уравнения S y
= 0 ![]() VT,1 = – VA,1 = –1/(2 м). Вычислив изгибающие моменты в характерных сечениях
рамы (у узлов L и С)
и учитывая, что в сечениях у шарниров А, Т, и Р моменты
равны нулю, строим эпюру М1 (рис. 4, б). Для контроля
проверяем равновесие моментов в узлах (рис. 4, в).
VT,1 = – VA,1 = –1/(2 м). Вычислив изгибающие моменты в характерных сечениях
рамы (у узлов L и С)
и учитывая, что в сечениях у шарниров А, Т, и Р моменты
равны нулю, строим эпюру М1 (рис. 4, б). Для контроля
проверяем равновесие моментов в узлах (рис. 4, в).![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 а) б)
а) б)