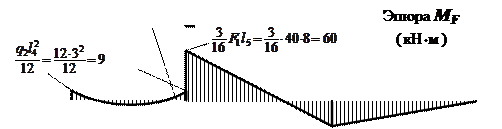









 а)
а)


б)
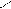
Q3,2 = – 3i0 ;
Q4,2 = – 4i0
;
Q5,2 = – (3/8) i0
|
|


поперечные силы
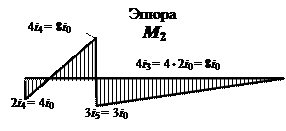
Q2 (рис. 23, б).
На рис. 24 представлены схема деформаций и
эпюра изгибающих моментов в третьем (от Z3 = 1) единичном состоянии основной
системы. Совместность перемещений
/ деформаций
элементов обеспечивается равенством вертикальных перемещений сечений e1
, b2 , е4 и b5 .

а)

 б)
б)

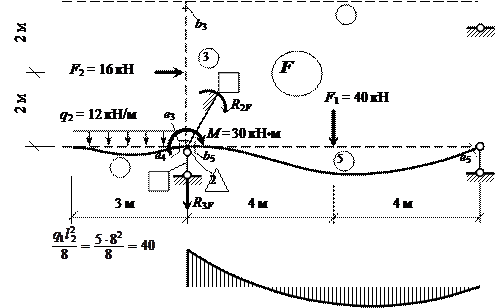
Рассматривая грузовое состояние основной
системы с приложенными к ней заданными нагрузками (рис. 25, а), по табл. 2 Приложения
определяем изгибающие моменты MF (рис.
25, б) и соответствующие им поперечные силы QF
(рис. 25, в).
Следует обратить внимание на то, что в
грузовом состоянии узлы ОСМП остаются неподвижными; каждый элемент деформируется
независимо от других – только от внеузловых нагрузок, приложенных
непосредственно к нему. Узловые нагрузки – вертикальная сила F2 в узле 1 и момент М
в узле 2 – не вызывают изгиба стержней.




а)













б)

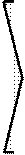



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а)
а)


![]()
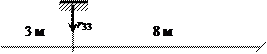
 б)
б) 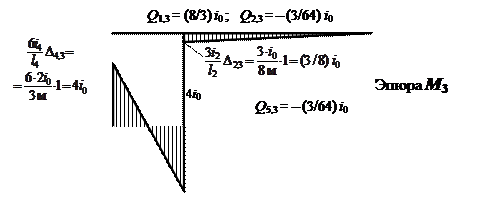
![]()