. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
|
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
|
|
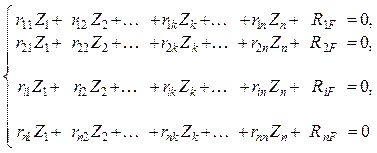
(2.7)
может быть представлена в матричной форме:
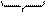
. . . . . . . . . . . . . . .
|
|
. . . . . . . . . . . . . . .
|
|
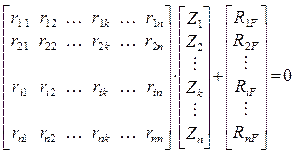
или
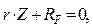
(2.8)
r Z RF
где
r –
матрица внешней жёсткости основной системы метода перемещений по направлениям основных неизвестных Z
(матрица единичных реакций связей,
введённых в расчётные узлы; коэффициентов при основных неизвестных);
Z – вектор*) основных неизвестных;
RF – вектор*) реакций введённых связей от
заданной нагрузки
(свободных
членов канонических уравнений);
n = nk , nk – степень кинематической неопределимости.
Матрицы r и RF вычисляются по
следующим формулам:
r = aт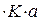 ;
(2.9)
;
(2.9)
RF = aт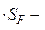 cт
cт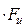 ; (2.10)
; (2.10)
где
a = [ a1 a2 … ai…an ]
– матрица перемещений концевых сечений элементов основной системы от единичных смещений введённых связей (столбцы a1, a2, …, an – соответственно от Z1 = 1,
Z2 = 1,
…, Zn = 1);
 *) При расчёте на несколько
(nV) вариантов заданных нагрузок Z и RF –
*) При расчёте на несколько
(nV) вариантов заданных нагрузок Z и RF –
матрицы, имеющие nV столбцов.
|
|
ai =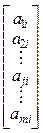
|
|
тов ОСМП в i-м единичном состоянии (от единичного смещения i-й связи, Zi = 1);
j – номер элемента; m – количество элементов;
|
|
– вектор перемещений концевых сечений элемен
aji – вектор перемещений концевых
сечений
j-го элемента от единичного смещения
i-й связи;
K –
матрица внутреннейжёсткости
основной системы, формируемая
как квазидиагональная из матриц жёсткости
элементов: K = diag [ K1 K2 … Kj … Km ];
ца с nV столбцами) усилий в концевых сечениях элементов ОСМП (концевых усилий) в грузовом
состоянии – от заданных нагрузок;
|
|
SF =
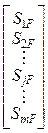
– вектор (при
поливариантном загружении – матри-
SjF – вектор (матрица)
концевых усилий j-го элемента в грузовом состоянии;
c = [ c1 c2 … ci … cn ] – матрица перемещений узлов основной системы от единичных смещений введённых связей
(столбцы с1,
с2, …, сn – соответственно от Z1 = 1, Z2 = 1, …, Zn =
1);
ном
состоянии (от смещения Zi =
1);
t – номер узла;
nu – число
узлов, перемещения которых могут быть отличными от нуля;
|
|
сi =
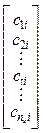
– вектор перемещений узлов ОСМП в
i-м
единич
cti – вектор компонентов перемещений
t-го узла от единич
Fu =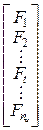 – –
|
|
ного
смещения
i-й связи;
вектор (или матрица с nV столбцами) заданных узловых нагрузок (сосредоточенных сил и моментов;
Ft – вектор (матрица) сосредоточенных нагрузок в t-м узле.
Структура матриц aji , Kj и SjF зависит от типа элемента ОСМП,
определяемого закреплениями его концов (шарнир, защемление) и видом
испытываемой им деформации (изгиб, растяжение - сжатие), –
см. табл. 3 Приложения.
Матрицы cti и Ft имеют следующий
вид:
а) для жёсткого узла б)
для шарнирного узла
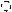
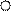

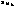









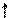

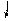





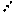
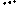



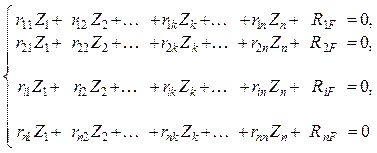 (2.7)
(2.7)
![]()
![]()
![]()
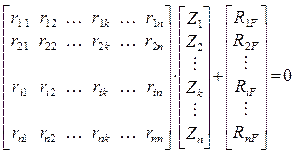 или
или
![]() ;
(2.9)
;
(2.9)![]() cт
cт![]() ; (2.10)
; (2.10)![]() *) При расчёте на несколько
(nV) вариантов заданных нагрузок Z и RF –
*) При расчёте на несколько
(nV) вариантов заданных нагрузок Z и RF –