Расчёт плоской статически неопределимой рамы методом сил. Расчёт плоской статически неопределимой рамы методом перемещений, страница 2

P

              а)                                              б)

	L
				C
			Т

 

в)                                              г)

Рис. 2

На рис. 2 представлены некоторые варианты основной системы для рассматриваемой рамы. Из них сразу следует исключить вариант «б» – в нём два диска ALC и CGP соединяются между собой и прикрепляются к диску «земля» тремя шарнирами А, С и Р, расположенными на одной прямой, – это признак мгновенной изменяемости системы, устранить которую часть СТ  не в состоянии.

Варианты «а», «в» и «г» формально возможны (все системы геометрически неизменяемые), но «а» и «в» следует признать менее удачными, чем «г», так как в них среди удалённых связей есть линейные, а более предпочтительным является удаление угловых связей.   

В узлах L и G в ОСМС – цилиндрические шарниры, возник-шие в результате удаления угловых связей в этих узлах. Следует об-ратить внимание на то, что основные неизвест-ные – парные (групповые); это равные, но противоположно напра-вленные изгибающие моменты в сечениях,    расположенных  беско-

F1

       Ещё один вариант – лучший, чем «г» на рис. 2, и поэтому принимаемый для дальнейшего расчёта, – показан на рис. 3.

 

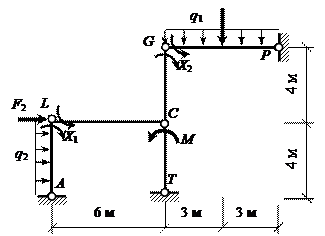                                                Рис. 3

нечно близко к введённому шарниру по разные стороны от него.

Выбранная ОСМС должна быть проверена на геометрическую неизменяемость. Для этого сначала выполняется её количественный анализ по необходимому (но недостаточному) условию геометрической неизменяемости , где W определяется по (1.1). Рассматривая стержни AL, TC, GP, а также ломаный стержень LCG  как диски, имеем D = 4. Эти диски соединены друг с другом тремя простыми шарнирами L, C и G (Н = 3). Внешних (опорных) связей шесть – по две в каждом из опорных шарниров A, Т и Р, т.е. С₀ = 6. Получаем W = 3 * 4 – 2 * 3 – 6 = 0 – необходимое условие неизменяемости ОСМС выполняется.   Теперь нужно проверить правильность структуры основной системы. Если прямолинейные стержни AL, TCи GP с шарнирами по концам считать линейными связями, то ОСМС можно рассматривать как результат прикрепления диска LCGк «земле» указанными тремя простыми связями, оси которых не пересекаются в одной точке – это геометрически неизменяемое соединение двух дисков. А поскольку один из дисков – «земля», то результат – геометрически неизменяемая система.

Заметим, что, несмотря на невозможность выделения в выбранной ОСМС главных и второстепенных частей, она будет более удобной, чем другие рассмотренные выше варианты, если учесть особенности заданных нагрузок: все они оказываются приложенными к элементам простейшего вида – однопролётным прямым стержням с шарнирами по концам.

3. Канонические уравнения

Канонические уравнения метода сил (КУМС), предназначенные для определения основных неизвестных Х₁ и Х₂ – реакций удалённых лишних связей, получаются из кинематических условий D₁ = 0 и D₂ = 0 – отрицания перемещений по направлениям удалённых жёстких лишних связей от совместного действия на основную систему заданных нагрузок и реакций лишних связей Х₁ и Х₂ . Расписывая перемещения D₁ и D₂  на основании принципа суперпозиции в виде D₁ = D_1X + D_1F  и D₂ = D_2X + D_2F , по-лучаем уравнения для определения Х₁ и Х₂  в каноническом виде:

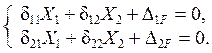                        (1.2)

Коэффициенты d_ik (i, k = 1, 2) при неизвестных Х₁ и Х₂  и сво-бодные члены D_iF (i = 1, 2) канонических уравнений – перемещения в основной системе по направлениям удалённых лишних связей (или, что то же самое, по направлениям основных неизвестных) от отдельно приложенных единичных неизвестных    Х₁ = 1,  Х₂ = 1  и заданной нагрузки.