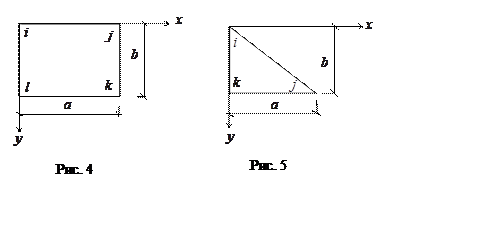
для прямоугольника.
Матрица ![]() строится подстановкой координат
узлов, которым задаются перемещения, в
строится подстановкой координат
узлов, которым задаются перемещения, в ![]() и ее
производных [
и ее
производных [![]() ].
].
При решении задачи узлы обходятся в последовательности
![]() . Сначала для каждого узла фиксируется
. Сначала для каждого узла фиксируется ![]() , затем
, затем ![]() и
и ![]() .
.
Матрица жесткости равна матрице
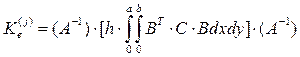 (33)
(33)
для прямоугольника,
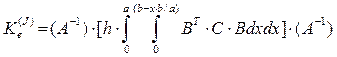 (34)
(34)
для треугольника.
Матрица ![]() – матрица деформаций, состоящая
из трех строк. Компоненты первой строки
– матрица деформаций, состоящая
из трех строк. Компоненты первой строки ![]() , второй
, второй
![]() , третьей –
, третьей – ![]() .
.
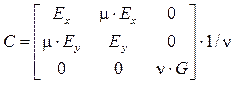 , (35)
, (35)
![]() .
.
Распределенная масса заменяется узловой. Узловые сосредоточенные
массы ![]() для прямоугольника равны произведениям примыкающих
к узлам площадям на интенсивность распределенной массы
для прямоугольника равны произведениям примыкающих
к узлам площадям на интенсивность распределенной массы ![]() .
Узловые сосредоточенные массы для треугольника определяются по правилу рычага
(массы распределяются между узлами обратно пропорционально длинам медиан) и
равны:
.
Узловые сосредоточенные массы для треугольника определяются по правилу рычага
(массы распределяются между узлами обратно пропорционально длинам медиан) и
равны:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Моменты инерции узловых масс условно принимаются равными ![]()
![]() , или нулю. В последнем
случае угловым связям, накладываемым на систему, присваиваются последние
порядковые номера.
, или нулю. В последнем
случае угловым связям, накладываемым на систему, присваиваются последние
порядковые номера.
Матрица ![]() – диагональная.
Диагональные элементы записываются в последовательности:
– диагональная.
Диагональные элементы записываются в последовательности:
![]() ,
, ![]() ,
, ![]() ,.
,.![]() .
.
Распределенная нагрузка заменяется узловой. Узловые силы определяются аналогично узловым массам.
Зависимость между усилиями и деформациями имеет вид:
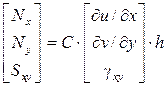 .
(36)
.
(36)
Нормальные усилия определяются для средин сторон четырех угольника, так как значения их больше чем в узлах. Сдвигающие усилия определяются в средней точке. В треугольнике усилия принимаются постоянными для всего элемента.
Вектор ![]() усилий равен вектору
усилий равен вектору
![]() (37)
(37)
для прямоугольного элемента (верхние индексы – стороны прямоугольника). Для треугольного элемента
![]() .
(38)
.
(38)
Вектор усилий, в случае узловой нагрузки и узловых сил инерции, определяется матричным произведением
![]() .
(39)
.
(39)
![]() – матрица распределенных усилий от
единичных смещений узлов. Компоненты
– матрица распределенных усилий от
единичных смещений узлов. Компоненты ![]() записываются в
последовательности:
записываются в
последовательности: ![]() .
.
Матрица преобразований ![]()
![]() ‑того
элемента в
‑того
элемента в ![]() ‑том узле от глобальной системы координат к
локальной определяется произведением
‑том узле от глобальной системы координат к
локальной определяется произведением
![]() ,
(40)
,
(40)
в котором ![]() матрица перемещений
матрица перемещений ![]() ‑того узла
‑того узла ![]() -того
элемента в глобальной системе координат, а
-того
элемента в глобальной системе координат, а
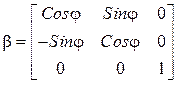 .
.
![]() – угол между глобальными и локальными
осями. Он отсчитывается против хода часовой стрелки, если смотреть из начала
координат глобальной системы.
– угол между глобальными и локальными
осями. Он отсчитывается против хода часовой стрелки, если смотреть из начала
координат глобальной системы.
1.5 Сооружения на упругом основании
Конструкция, в том числе и основание, разбивается на элементы.
Элементам основания присваивается тип, одинаковый с типом расположенного на нем
конструктивного элемента. Перемещения узлов основания принимаются равными
перемещениям расположенного на нем конструктивного элемента. Влияние упругих
сил основания заменяются эквивалентными узловыми силами исходя из равенства
работ узловых и распределенных сил. В случае винклеровского основания давление
со стороны основания на точку расположенного на нем элемента равно ![]() .
. ![]() –коэффициент
упругого основания. Матрица узловых сил, в этом случае, равна матрице
–коэффициент
упругого основания. Матрица узловых сил, в этом случае, равна матрице
![]() (41)
(41)
и определяется по формулам для ![]() подстановкой
в них вместо интенсивности распределенной массы коэффициента
подстановкой
в них вместо интенсивности распределенной массы коэффициента ![]() .
.
Реакции основания от единичных смещений узлов равны
![]() .
(42)
.
(42)
В уравнениях для определения основных неизвестных
![]() =
=![]() (43).
(43).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.