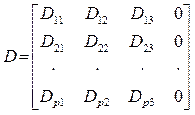В.И. Роев. Расчет статически и динамически нагруженных систем с использованием программного комплекса DINAM, страница 4

                                                                                                                                                                         

                                .                                                   

          

 – значения  компоненты   вектора  в начале, средине и конце интервала  .

 в этом случае можно задать произведением              

                                                                  (5)

в котором  – матрица порядка  постоянных коэффициентов.

Подставляя (5) в (3), получим:

            (6)                              

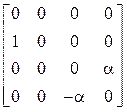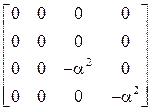    =,  =, /T.

Уравнение (6) – система двух матричных уравнений,

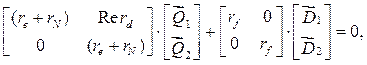                                                                                                                                                                                                                     (7)                  

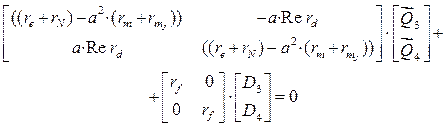
В случае гармонических возмущений , компоненты двух первых столбцов матрицы  равны нулям, компоненты третьего столбца равны амплитудным значениям заданных возмущений. Поэтому                              

                          .

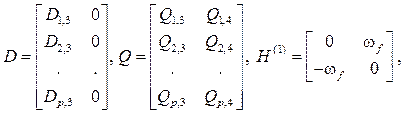
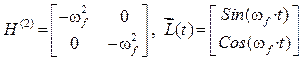Уравнение (6) трансформируется в уравнение                         

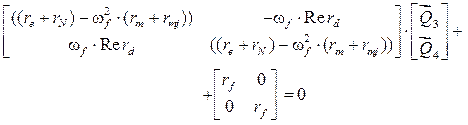    (8)

Для консервативных систем (6) трансформируется в уравнение                                     

              ,             (9)                                    ,     

                             .

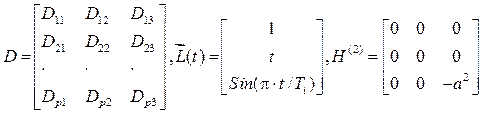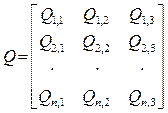Компоненты  определяются из уравнений                                         

                            ,

                                     ,

                       .

Амплитудные значения  в случае гармонических возмущений консервативных систем определяются из уравнения

                         .               (10)

Стационарные колебания диссипативных систем при гармонических возмущениях описываются частным решением (3). За интервал принимается . Компоненты двух первых столбцов матрицы  равны нулям. Компоненты третьего  столбца равняются амплитудным значениям   заданных возмущений.  преобразуются в матрицы

                                 

                

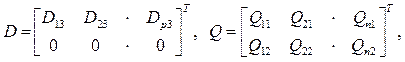
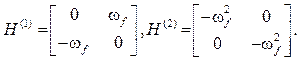
Вектор  трансформируется  в вектор

                           .

Уравнение (6) превращается в систему уравнений

         ,                                                        .

Компоненты равны соответственно компонентам  первого и второго столбцов матрицы . Компоненты  равны компонентам первого столбца матрицы .

        Расчет на мгновенный импульс состоит из двух этапов. На первом этапе решается уравнение

                                 ,                  (11)

в котором  вектор заданных мгновенных импульсов.

На втором этапе заданная система рассчитывается на свободные колебания с  начальными условиями :                                          

                            .

1.2  . Стержневые системы

                            Изгиб, растяжение, кручение.                          

     Изгибаемый стержень, жестко соединенный с узлами  

   Деформированное состояние стержня определяется углами поворота  концевых сечений и их линейными  смещениями  по нормали к его оси.  Положительные направления перемещений и концевых усилий показаны на рис. 1.

Рис. 1

Матрица  перемещений поперечных сечений стержня с защемленными концами определяется матричным произведением  

    .         (12)                                                                                                                                                                                                                                                                                                

                     

           ,                                                                 

                   =1                                                 

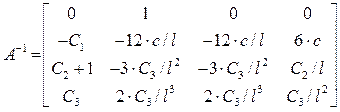         =1 – 6*c,       *c,     =1- 12*c

                    

для элементов сплошного сечения.

Для элементов сквозного сечения

                                .