![]()
Решение задачи состоит из двух этапов. На первом этапе определяются скорости узлов – начальные условия. На втором этапе заданная система рассчитывается на собственные колебания.
Первый этап. Компоненты шестых столбцов матриц ![]() - концевые усилия в элементах основной
системы от заданных импульсов. Они определяются как усилия от статической нагрузки.
Компоненты седьмых столбцов принимаются равными нулю. В матрице
- концевые усилия в элементах основной
системы от заданных импульсов. Они определяются как усилия от статической нагрузки.
Компоненты седьмых столбцов принимаются равными нулю. В матрице ![]() мгновенному импульсу соответствует
мгновенному импульсу соответствует ![]() .
.
Исходные данные: Матрицы ![]() такие же, как в предыдущей
задаче.
такие же, как в предыдущей
задаче.
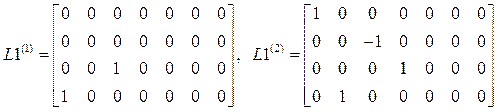 ,
, 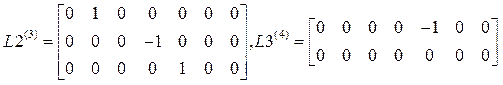 ,
,
![]() .
.
Результаты расчета. На печать выдаются матрицы ![]() .
. ![]() такие
же как в задаче на гармонические возмущения.
такие
же как в задаче на гармонические возмущения.
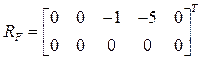 .
.
Из уравнения ![]() определяется матрица
обобщенных координат и их первых производных в момент исчезновения импульсов
определяется матрица
обобщенных координат и их первых производных в момент исчезновения импульсов
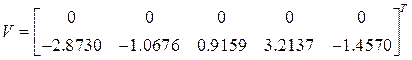 .
.
После нажатия клавиши ![]() осуществляется переход
ко второму этапу.
осуществляется переход
ко второму этапу.
Второй этап расчета.
На экран выдаются исходные данные первого этапа расчета и матрица ![]() . В матрице
. В матрице ![]()
![]() заменяется на
заменяется на ![]() . По
желанию пользователя в матрицах
. По
желанию пользователя в матрицах ![]() компоненты столбцов,
соответствующих концевым усилиям от статических и динамических возмущений можно
откорректировать. В рассматриваемом примере это компоненты шестых и седьмых
столбцов. Для того, чтобы определить усилия от статической нагрузки
компоненты столбцов,
соответствующих концевым усилиям от статических и динамических возмущений можно
откорректировать. В рассматриваемом примере это компоненты шестых и седьмых
столбцов. Для того, чтобы определить усилия от статической нагрузки ![]() компоненты шестых столбцов матриц
компоненты шестых столбцов матриц![]() приняты равными 10 и 15 соответственно.
Начальными условиями являются компоненты матрицы
приняты равными 10 и 15 соответственно.
Начальными условиями являются компоненты матрицы ![]() .
.
Результаты расчета. На печать выдаются матрицы ![]() , матрицы обобщенных координат, их вторых
производных, концевые усилия в моменты времени, соответствующие границам
отрезков, начальные условия на границах интервалов, векторы частот и периодов
собственных колебаний.
, матрицы обобщенных координат, их вторых
производных, концевые усилия в моменты времени, соответствующие границам
отрезков, начальные условия на границах интервалов, векторы частот и периодов
собственных колебаний.
На границах отрезков первого интервала концевые усилия первого элемента образуют матрицу
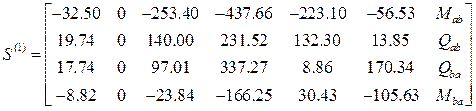 .
.
На границах отрезков второго интервала концевые усилия образуют матрицу
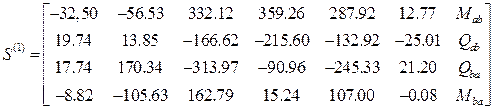 .
.
Начальные условия второго интервала определяются матрицей
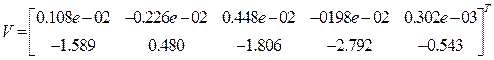 .
.
Матрица перемещений и скоростей
в конце второго интервала имеет вид: 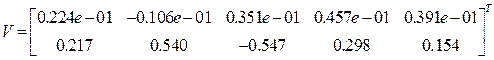 .
.
Определение усилий в диссипативных системах.
Определить усилия в диссипативной системе на рис. 6 от заданных возмущений.
Коэффициенты внутреннего трения в первом, втором и третьем элементах ![]() =0.02. Влиянием внутреннего трения остальных
элементов пренебрегаем.
=0.02. Влиянием внутреннего трения остальных
элементов пренебрегаем.
В расчетах диссипативных систем M1(12) = 7. Компоненты седьмых столбцов матриц EI равны коэффициентам внутреннего трения.
Остальные компоненты указанных матриц равны фактическим значениям соответствующих величин.
Матрицы LI составляются так же, как и в расчетах без учета внутреннего трения.
P1 = ![]()
![]() EJ
EJ![]() ,
, ![]() = k/EA,
R1 = N/EJ
= k/EA,
R1 = N/EJ![]()
С учетом сказанного матрицы M1, E1, E2, E3 и E4 имеют вид:
E1=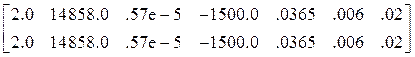 ,
,
E2=![]() ,
,
E3=![]() ,
,
E4=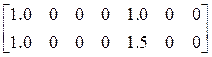 .
.
Основные неизвестные определятся из уравнения:
![]()
![]() (t) +
(t) + ![]()
![]() (t) +
(t) + ![]() +
+![]() = 0,
= 0,
от гармонических возмущений в моменты
времени : ( 0, .707, 1.00, .707, 0 )*Т , (Т = 0,5*![]() ,
, ![]() =53.0 р/с);
=53.0 р/с);
![]() +
+ ![]() =
0
=
0
от статических возмущений.
Усилия в заданные моменты времени в элементах заданной системы определяются по формуле (18) первой части пособия. Они образуют матрицы:
r![]() =
=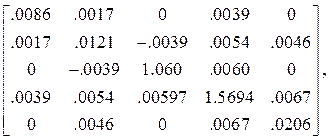
r![]() =
=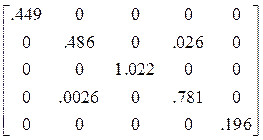 ,
,
r![]() =
=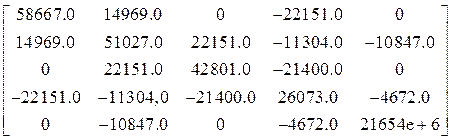 ,
,
R![]() =
= 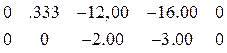
.Матрица Z обобщенных координат равна матрице:
Z= 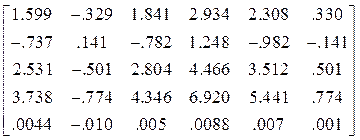 *10
*10![]() .
.
Матрица Z![]() первых производных
первых производных
Z![]()
![]() =
= 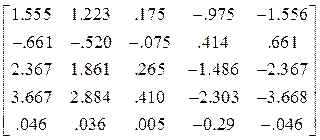 *10
*10![]() ,
,
Матрица Z![]() вторых
производных
вторых
производных
Z![]() =
=
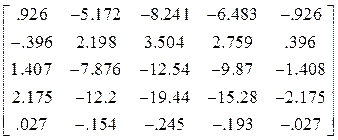 .
.
Матрицы усилий в элементах заданной системы :
Первый элемент
M![]() ; -32.45
6.17 -34.56 -55.05 -43.28 -6.17
Q
; -32.45
6.17 -34.56 -55.05 -43.28 -6.17
Q![]() ;
19.73 -3.42 19.24 30.63 24.08 3.42
Q
;
19.73 -3.42 19.24 30.63 24.08 3.42
Q![]() ;17.73-3.2219.1430.2923.693..22
M
;17.73-3.2219.1430.2923.693..22
M![]() ; -8.81 1.52 -7.97
-12.79 -10.12 -1.52
; -8.81 1.52 -7.97
-12.79 -10.12 -1.52
Второй элемент
M![]() ; 8.81 -1.51 7.97 12.79 10.12 1.52
Q
; 8.81 -1.51 7.97 12.79 10.12 1.52
Q![]() ; 7.73 - 1.81 9.85 15.74 12.42
1.8
; 7.73 - 1.81 9.85 15.74 12.42
1.8
Q![]() ;5.73 -1,41 9.23 14.46 11.22 1.41
;5.73 -1,41 9.23 14.46 11.22 1.41
M![]() ; -24.09 5. 31 -29.33 -46.80 -36.85 -5.31
; -24.09 5. 31 -29.33 -46.80 -36.85 -5.31
Третий элемент
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.