3.2. Расчет тонкой плиты
на статические и гармонические возмущения
В защемленной по контуру железобетонной плите (рис.14) определить
усилия от статических нагрузок ![]() ,
, ![]() и амплитудные значения усилий от гармонической
нагрузи F(t)
и амплитудные значения усилий от гармонической
нагрузи F(t)![]() =1.0*Sin(148*t) kH, приложенных в центре плиты.
=1.0*Sin(148*t) kH, приложенных в центре плиты.
![]() .
.![]()
![]() ,
,![]() ,
,
![]() .
.
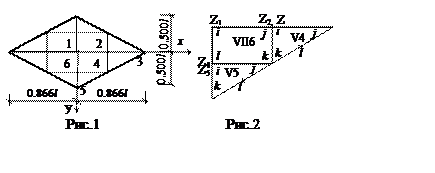
Рис.14 Рис.15
Учитывая симметрию, усилия определим в четверти заданной системы (рис.15). Выделенную часть в расчете представим шестью элементами. Узлы 1, 2, 6 с сосредоточенными силами – элементы четвертого типа с порядковыми номерами 1, 2, 3. Треугольники 234,456 (рис.14)– элементы пятого типа с порядковыми номерами V4, V5 (рис.15). Прямоугольный элемент 1246 –элемент седьмого типа, порядковый номер VII-6.
На первый элемент действует статическая сила ![]() и динамическая - с амп-
и динамическая - с амп-
литудным значением ![]() .
На второй и третий статические силы
.
На второй и третий статические силы ![]() .
.
Исходные данные:
M1 = [ 0 0 5 2 0 0 0 0 3 0 0 5 2 0 0 1 2 0
1 0 ]
E4 =![]()
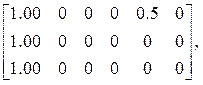
Lx Ly Dx Dy Dm Dk ![]()
![]()
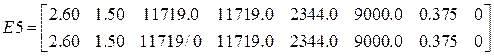 ,
,
Lx Ly Dx Dy Dm Dk ![]()
![]()
![]()
Матрицы L4, L5, L7: ![]()
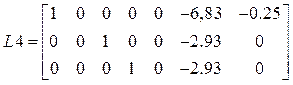 ,
,
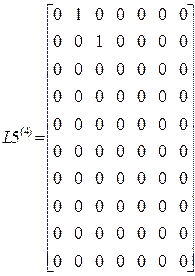 ,
, ![]() =
= 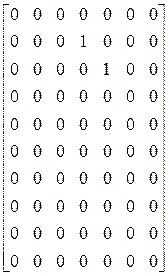 ,
, 
![]() Δ
Δ![]()
![]()
![]() Δ
Δ![]()
![]()
![]() Δ
Δ![]()
![]()
![]()
![]()
![]()
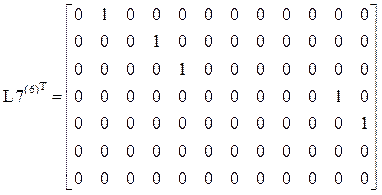
Компоненты первых пяти строк матрицы L7 – перемещения узлов.
Компоненты шестой и седьмой строк – усилия в элементах основной системы от заданной нагрузки.
Результаты расчета.
Матрицы реакций ![]()
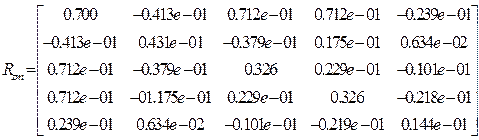 ,
,
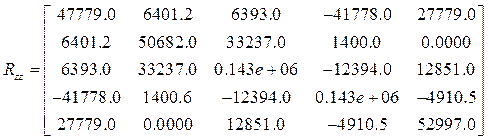 ,
,
R![]() =
=
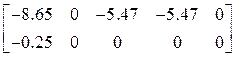 .
.
Коэффициенты жесткостей узлов элементов при повороте относительно координатных осей:
Четвертый элемент b(I,y)=37506.0, b(I,x)=24526.0, b(j,y)=8156.4, b(j,x)=12602.0, b(k,y)=28263.0, b(k,x)=21682.0.
Пятый элемент b(I,y)=37506.0, b(I,x)=24526.0, b(j,y)=8156.4, b(j,x)=12602.0, b(k,y)=28263.0, b(k,x)=21682.0.
Шестой элемент b(I,y)=13175.0, b(I,x)=47779.0, b(j,y)=13175.0, b(j,x)=47779.0, b(k,y)=13175.0, b(k,x)=47779.0.
Вектор собственных чисел λ и матрица V собственных векторов
![]() *e-08
*e-08
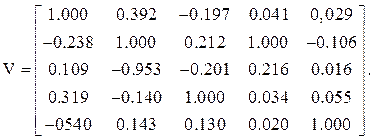
Матрица [ Z ] ,увеличенных в 1.0*E3 раз, перемещений узлов заданной системы
Z ![]() =
=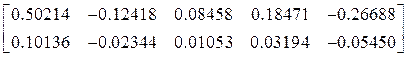 .
.
Матрица ![]() усилий в элементах
заданной системы:
Четвертый и пятый элементы
усилий в элементах
заданной системы:
Четвертый и пятый элементы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=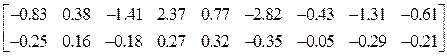
![]() =
=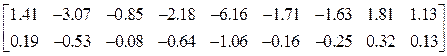
Шестой элемент основной системы
M![]() M
M![]() M
M![]() M
M![]() M
M![]() M
M![]() M
M![]() M
M![]() M
M![]() M
M![]() M
M![]()
![]() =
=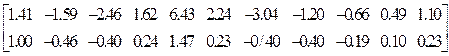 .
.
Положительные изгибающие моменты растягивают нижние волокна.
Восьмые и девятые компоненты матриц ![]() ,
,
![]() изги-
изги-
бающие моменты в центрах четвертого и
пятого элементов. Десятые и одиннадцатые компоненты ![]() - изгибающие
моменты в центре пятого элемента. Изгибающие моменты в узловых точках
определяются как средние значения моментов в узлах смежных элементов.Компоненты
первых строк матриц Z
- изгибающие
моменты в центре пятого элемента. Изгибающие моменты в узловых точках
определяются как средние значения моментов в узлах смежных элементов.Компоненты
первых строк матриц Z![]() , S
, S![]() - перемещения и усилия от
постоянной нагрузки, вторых – от временной нагрузки.
- перемещения и усилия от
постоянной нагрузки, вторых – от временной нагрузки.
Изгибающие моменты на границе четвертого и шестого элементов относительно осей Y и X равны ((-0.83)+(-1.59)):2 = -1.21 кНм, (2.37+2.24):2 = 2,31 кНм; на границе пятого и шестого - (1.41+1.61):2 = 1.52 кНм, ((-2.18)+(-1.20)):2 = -1.69 кНм; на границе четвертого, пятого и шестого: ((-1.41) + (-3.06) + (-2.46)): 3 = -2.31 кНм, ((-2.82) +(-6.16)+(-3.04)): 3 = -4.01 кНм.
3.3 Расчет железобетонной плиты на винклеровском основании.
На железобетонную плиту 8.00 х 4.00 х 0.30 м ., EJ![]() = EJ
= EJ![]() =94320 kHм, D
=94320 kHм, D![]() =18864 kHм,
D
=18864 kHм,
D![]() =72000 kНм,
=72000 kНм,
![]() = 0.2 на винклеровском основании с
коэффициентом упругой податливости 13012 кН/м
= 0.2 на винклеровском основании с
коэффициентом упругой податливости 13012 кН/м![]() (рис.16)
действуют: в центре плиты- сосредоточенные силы F
(рис.16)
действуют: в центре плиты- сосредоточенные силы F![]() =1000.0 kH, F(t)
=1000.0 kH, F(t)![]() =0.8*Sin(20*t) kH; в точках с координатами 2.0х 0 м и -2.0х0 (начало в центре плиты) сосредоточенны силы F= 400 kH. Собственный вес плиты 7.5 кН/м
=0.8*Sin(20*t) kH; в точках с координатами 2.0х 0 м и -2.0х0 (начало в центре плиты) сосредоточенны силы F= 400 kH. Собственный вес плиты 7.5 кН/м![]() .
.
![]() Требуется определить усилия от статических
возмущений и амплитудные значения усилий от динамических возмущений. Так как
заданная система симметричная то в расчете можно рас смотреть четверть плиты
(рис.17)
Требуется определить усилия от статических
возмущений и амплитудные значения усилий от динамических возмущений. Так как
заданная система симметричная то в расчете можно рас смотреть четверть плиты
(рис.17)
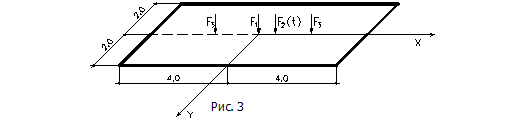
Рис.16
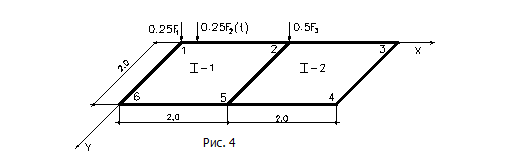
Рис.17
На выделенную часть действуют:
статические силы - F![]() =257.50 кН (узел 1), F
=257.50 кН (узел 1), F![]() =215.00 кН (узел 2) и динамическая–F(t)=0.2*Sin(31*t)
кН (узел 1).
=215.00 кН (узел 2) и динамическая–F(t)=0.2*Sin(31*t)
кН (узел 1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.