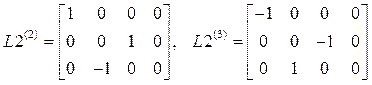В.И. Роев. Расчет статически и динамически нагруженных систем с использованием программного комплекса DINAM, страница 16

,

,                 

.

Результаты расчета:          

,

,                                                                  

/,                , 

,              .

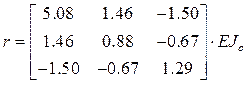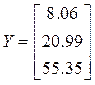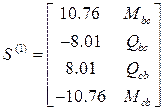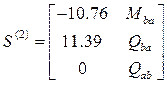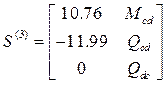                         2.3 Динамические возмущения

         Определение усилий от гармонических возмущений.

Система на рис. 6 находится под действием сил:                                   

               кН/м,,                          

              ,=53.00 р/с,   

                                           .

В сечении  находится точечная масса 1 т, в сечении  - точечная масса 1.5 т. Интенсивность распределенной массы балки – 0.0365 т/м, интенсивность распределенного момента инерции массы – . Требуется определить с учетом деформации сдвига по деформированной схеме усилия от статических составляющих заданных нагрузок, амплитудные составляющие от гармонических составляющих и их возможных сочетаний. Определить частоты и векторы форм собственных колебаний. Основная система на рис. 7

Исходные данные: В расчетах по деформированной схеме . Относительный угол сдвига  (- коэффициент формы поперечного сечения).

, .

                    

,                                                      

,                                          

.

 .                                                              

.

.

.

 

,

.

.

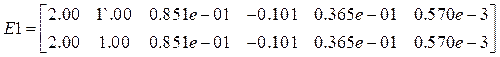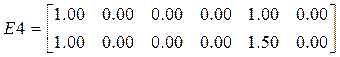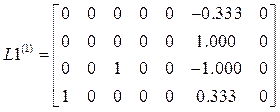
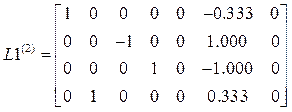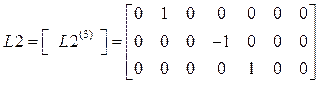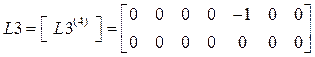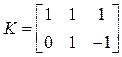Число определяемых собственных чисел 5.

.

Результаты расчета:

,

,

.

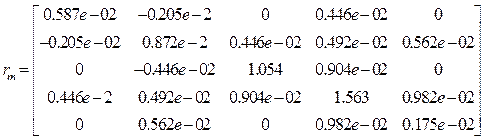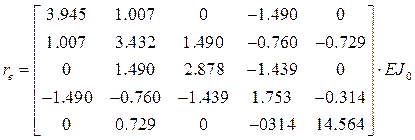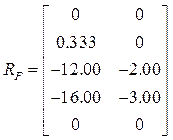Вектор собственных чисел:   

,

Матрица собственных векторов:

.

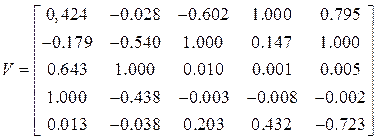Матрица основных неизвестных:

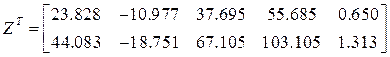
Матрицы концевых усилий: ,

,

 ,

,

,

                                   .

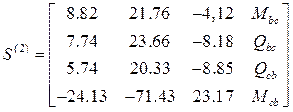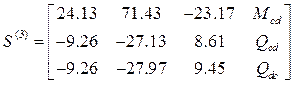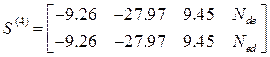Определение усилий от возмущений, изменяющихся

         во времени по произвольному закону(рис.13) 

На систему на рис. 6 действуют силы                                                                          

              F(t)=(10+5Sin(21.372t)) кН (0t0.147 с),

              F(t)=(15+1Sin(10.686t)) кН (0t0.588 с) ,                                 

                                F = 1500   .

 Определить усилия в моменты времени (0+0.0368n) с.  и (.294+.0735n) с. (0n4).

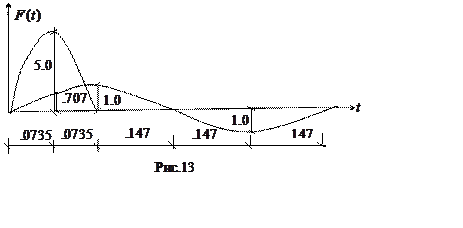
Основная система метода перемещений на рис. 2. . Время действия заданных возмущений разбиваем на три интервала длиной 0.147, 0.147, 0.294 с. Каждый интервал делим на 4 отрезка.

Исходные данные:                           

.

Матрицы  такие же как в расчетах на гармонические возмущения.

,

,

,

                            ,

.

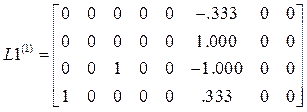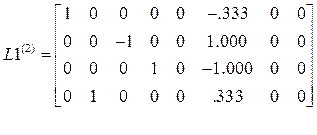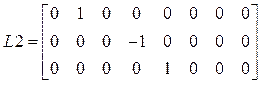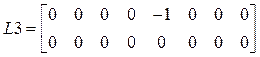Матрица начальных условий первого интервала (компоненты первого столбца – перемещения узлов, второго – скорости)

.

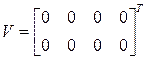Матрица длин интервалов      .

Матрица значений нагрузок в начале средине и конце интервалов

.

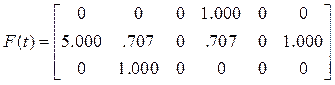Матрица дополнительных перемещений и скоростей, задаваемых в начале последнего интервала

.

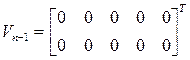Значения масштабной жесткости и масштабной массы                                           

 

.

Результаты расчета:

Матрицы  такие же как в расчетах на гармонические возмущения.

.

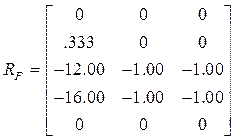Вектор собственных чисел и матрица собственных векторов такие же как в расчетах на гармонические возмущения.

Векторы частот и периодов собственных колебании                                         ,

Первый интервал.

Матрицы ускорений и увеличенных в раз перемещений узлов:

              ,                                              .

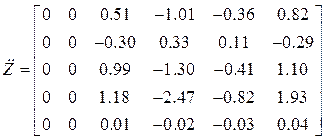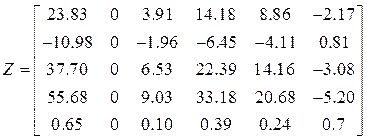Матрицы концевых усилий 

                  

,

,

,

,

.

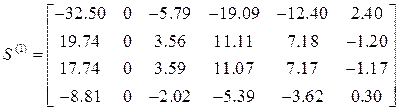
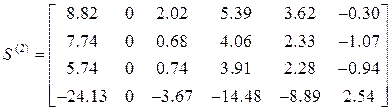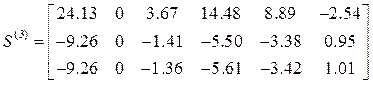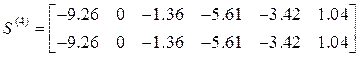Компоненты первых столбцов матриц   – ускорения, перемещения, концевые усилия от статических нагрузок. Компоненты остальных столбцов–ускорения, перемещения и концевые усилия от динамических возмущений в моменты времени, соответствующие границам отрезков.

Второй интервал. Матрица начальных условий                                     .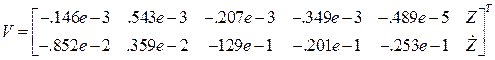

Матрицы       

,

,

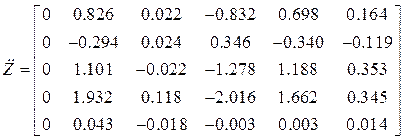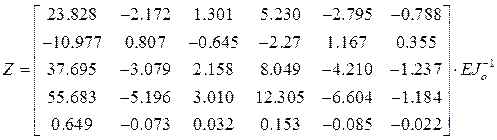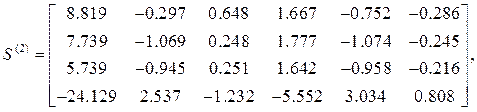
           Определение усилий от мгновенного импульса

Определить по деформированной схеме с учетом деформации сдвига усилия в системе на рис. 6, вызванные сосредоточенными мгновенными импульсами

                

в моменты времени 0.01395 (n = 0, 1, 2, …,8). Жесткости элементов системы и величины масс такие же как и в расчетах на нагрузку, изменяющуюся во времени по произвольному закону. Основная система на рис.7.

Заданное время разделим на два интервала. Число отрезков в интервале примем равным четырем.