Основную систему получим наложением на выделенную часть тринадцати связей: линейной - на узел 1; связей, препятствующих повороту узла 2 относительно оси Y и его вертикальному перемещению; связей, препятствующих повороту узла 3 относительно оси Y и его вертикальному перемещению; связей, препятствующих повороту четвертого узла относительно оси Y, его вертикальному перемещению и связи, препятствующей его повороту относительно оси X; связей, препятствующих повороту пятого узла относительно оси Y, его вертикальному перемещению и повороту относительно оси X; связей, препятствующих вертикальному перемещению шестого узла и его повороту относительно оси X.
Полученная основная система (рис.17 )состоит из десяти элементов: шесть элементов четвертого типа (узлы 1, 2, 3, 4, 5, 6) и четыре элемента седьмого типа: седьмой и восьмой–элементы 1-
2-5-6 плиты и элемент основания, девятый и десятый – элемент 2-3-4-5 плиты и элемент основания.
M1 = 
,
EA/EJ
P1R1M/MM
/M
E4 =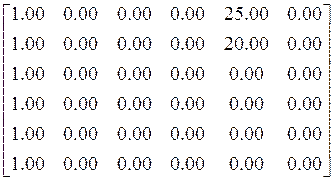 
МатрицаЕ7
Lx Ly Dx Dy Dm Dk M/Mo M/Mo
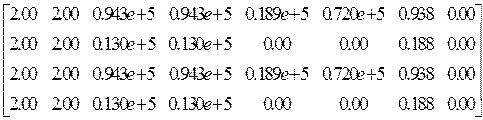
В матрицах L4 и L7 приведены только отличные от нуля компоненты. После компоненты указаны ее номер строки и номер столбца. Матрица L4 Первый элемент: 1.00(1,1), -257.50(1,14), -0.80(1,15); второй элемент : 1.00(2,3), -215.00(2,14), 0 (2,15) ; третий элемент : 1.00(3,5), -7.50 (3,14), 0(3,15) ; четвертый элемент: 1.00(4,7), -7.50 (4,14), 0(4,15) пятый элемент: 1.00(5,10), -15.00(5,14), 0(5,15) ; шестой элемент : 1.00(6,12), -7.50(6,14), 0(6,15) .
Матрица L7
7-ой элемент: 1.00(2,1), 1.00(4,2), 1.00(5,3), 1.00(7,9), 1.00(8,10),
1.00(9,11), 1.00(11,12), 1.00(12,13);
8-ой элемент: 1.00(2,1), 1.00(5,3), 1.00(8,10), 1.00(11,12);
9-ый элемент: 1.00(1,2), 1.00(2,3), 1.00(4,4), 1.00(5,5), 1.00(7,6), 1.00(8,7),
1.00(9,8), 1.00(10,9), 1.00(11,10), 1.00(12,11);
10-ый элемент: 1.00(2,3), 1.00(5,5), 1.00(8,7), 1.00(11,10).
= 31.00 р/сек, EJ=1.00,
m=1.00 .
Компоненты первых строк матриц R
,
R
образуют матрицы:
R
=
R
=
Матица R
равна
матрице:
R=
.
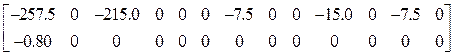Первые три собственных числа образуют вектор :
=[
0.761 0.127 0.019 ]e-03, а одиннадцатое, двенадцатое и тринадцатое –вектор :
=[
0.630 0.559 0.402 ]e-07.
Им соответствуют собственные векторы :
Матрица Z перемещений узлов заданной системы ( матрица основных неизвестных): 1; 0.840е-02 0.627e-04 2; -0.199e-02 -0.174e-04 3; 0.596e-02 0.392e-04 4; -0.238e-02 -0.184e-04 5; 0.144e-02 0.304e-05 6; -0.202e-02 -0.164e-04 7; 0.966e-03 0.115e-06 8; -0.388e-03 -0.242e-05 9; -0.157e-02 -0.137e-04 10; 0.473e-02 0.316e-04 11; -0.872e-03 -0.549e-05 12; 0.623e-02 0.467e-04 13; -0.135e-02 -0.108e-04
Матрица S усилий в элементах заданной системы.
Усилия в элементах четвертого типа от статических возмущений в заданной системе равны усилиям в элементах заданной системы. Амплитудные значения усилий от динамических возмущений отличны от нуля в первом и втором элементах и равны:
S
=-2.306 кН, S
=-0.753 кН.
Усилия от статических и динамических возмущений в седьмом и девятом элементах образуют матрицы:
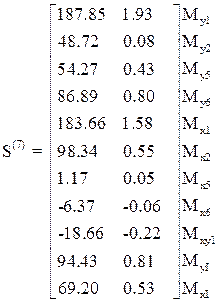
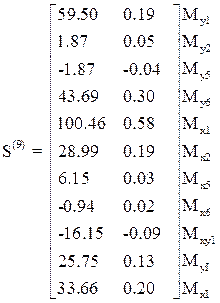
Интенсивность давления на основание определяется произведением
жесткости основания на смещения линейных связей:
в узле 1 .130е5*(.840е-02 .626е-04) = ( .109 .008)е3кН/м
,
в узле 2 .130е5*(.596е-02 .392е-04) = ( .077 .005)е3 кН/м,
в узле 3 .130е5*(.144е-02 .304е-05) = ( .018 0.001)е3кН/м,
в узле 4 .130е5*(.996е-03 .115е-06) = ( .013 .001)е2 кН/м,
в узле 5 .130е5*(.473е-02 .316е-04) = ( .058 .004)е3 кН/м,
в узле 6 .130е5*(.643е-02 .467е-04) = ( .083 .006)е3 кН/м
4. Плоская задача теории упругости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.