![]() – интенсивность распределенной массы.
– интенсивность распределенной массы.
Распределенная нагрузка заменяется узловой. Эквивалентная узловая нагрузка определяется из условия равенства возмож
ных работ узловых сил и заданной распределенной нагрузки.
В случае равномерно распределенной нагрузки узловые сосредоточенные
силы ![]() для прямоугольного элемента равны произведению
примыкающей к узлу площади на интенсивность нагрузки.
для прямоугольного элемента равны произведению
примыкающей к узлу площади на интенсивность нагрузки.
Для треугольного элемента они равны
![]() ,
,
![]() .
.
Зависимость между изгибающими моментами и деформациями:
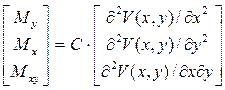 . (24)
. (24)
Изгибающие моменты являются линейными функциями координат и
определяются в узловых точках. Крутящие моменты изменяются нелинейно и
определяются в центре прямоугольного элемента и в точке ![]() треугольного
элемента.
треугольного
элемента.
Вектор усилий ![]() равен
равен
![]()
![]() (25)
(25)
для прямоугольного элемента и
![]()
![]() ( (26)
( (26)
для треугольного элемента.
Первый индекс – номер узла, второй – ось, относительно которой действует момент. Знак плюс у изгибающих моментов показывает, что растянуты нижние волокна .
Вектор усилий, в случае узловой нагрузки и узловых сил инерции, определяется матричным произведением
![]() . (27)
. (27)
![]() – матрица распределенных усилий от
единичных смещений узлов. Для прямоугольного элемента она определяется матрицей
– матрица распределенных усилий от
единичных смещений узлов. Для прямоугольного элемента она определяется матрицей
![]() . (28)
. (28)
Для треугольника матрица ![]() равна матрице
равна матрице
![]() .(29)
.(29)
Векторы ![]() (
(![]() ) –
векторы девятого порядка для прямоугольника и седьмого порядка для треугольника
Их компоненты зависят от жесткостных характеристик и размеров элемента.
) –
векторы девятого порядка для прямоугольника и седьмого порядка для треугольника
Их компоненты зависят от жесткостных характеристик и размеров элемента.
Компоненты ![]() того
того ![]() столбца
матрицы
столбца
матрицы ![]() записываются в последовательности:
записываются в последовательности: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для прямоугольника
и в последовательности:
для прямоугольника
и в последовательности: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для треугольного элемента.
для треугольного элемента.
Найденные усилия относятся к отдельным элементам. Они, как правило, имеют разные значения для элементов, примыкающих к одному и тому же узлу. Чтобы вычислить действитель
ный момент в узловой точке, нужно взять среднее значение от узловых моментов примыкающих к узлу элементов. Если элементы одинаковы, то сумма соответствующих моментов делится на число элементов, сходящихся в узле. Если же элементы имеют разную толщину и размеры, то действительный момент в точке определяется как сумма соответствующих моментов, умноженных на свои коэффициенты влияния, вычисляемые по формуле
![]() .
(30)
.
(30)
![]() – жесткость
– жесткость ![]() ‑того
элемента узле
‑того
элемента узле ![]() , соответствующая его единичному
повороту относительно оси
, соответствующая его единичному
повороту относительно оси ![]() .
.
Матрица преобразований ![]() от глобальной системы
координат к локальной определяется произведением
от глобальной системы
координат к локальной определяется произведением
![]() ,
(31)
,
(31)
в котором ![]() – матрица перемещений
– матрица перемещений ![]() ‑того узла
‑того узла ![]() ‑того
элемента в глобальной системе координат, а
‑того
элемента в глобальной системе координат, а
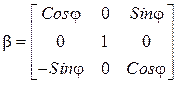 .
.
![]() – угол между глобальными и локальными
осями. Он отсчитывается против хода часовой стрелки, если смотреть из начала
глобальной системы координат.
– угол между глобальными и локальными
осями. Он отсчитывается против хода часовой стрелки, если смотреть из начала
глобальной системы координат.
Допустим, что в глобальной системе координат перемещения ![]() ‑того узла образуют матрицу
‑того узла образуют матрицу
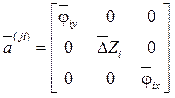 ,
, ![]() .
.
Тогда
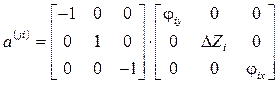 .
.
Если ![]() ,то
,то
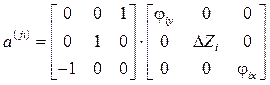 .
.
В заключение следует отметить: рассмотренная аппроксимация прогибов дает достаточно точные результаты, хотя и допускает разрыв деформаций в углах поворота между смежными элементами. Решение получается приближенным. Степень приближения зависит от числа и вида элементов, на которые разбит конструктивный элемент, а также от градиента заданных возмущений.
1.4. Плоская задача теории упругости
Заданная система разбивается на прямоугольники и прямоугольные треугольники (рис. 4 ,рис. 5).
Каждый узел имеет три степени свободы: два линейных и одно угловое
перемещение. Прямоугольная матрица ![]() определяется матричным
произведением:
определяется матричным
произведением:
![]() , (32)
, (32)
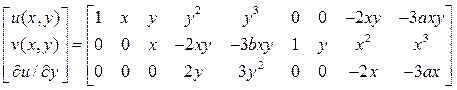
для треугольника и
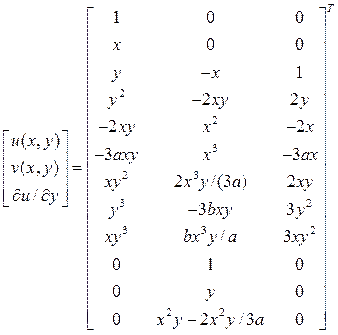
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.