В.И. Роев. Расчет статически и динамически нагруженных систем с использованием программного комплекса DINAM, страница 12

В элементах пятого ( треугольный элемент плиты)                               

,                                                     .

 – угол поворота узла  в плоскости, нормальной к прямой .

В элементах восьмого типа (прямоугольный элемент плоской задачи)                               

,            

.

 – перемещения узлов в направлении осей .  – угол поворота узла. Положительные перемещения совпадают с положительными направлениями локальных осей. Положительный угол поворота – поворот против хода часовой стрелки, если смотреть в начало координат.  – концевые усилия в узле.

Положительные концевые усилия направлены в сторону положительных локальных осей. Они по величине равны узловым силам и направлены в обратную сторону.

В элементах шестого типа (треугольный элемент плоской задачи)                                       

     ,                              

    .

4. Матрица сочетаний. Матрица сочетаний заданных возмущений – прямоугольная матрица. Число ее строк равно числу независимых заданных возмущений. Число столбцов – числу сочетаний заданных возмущений, интересующих пользователя. Компонента  ‑того столбца и ‑той строки равна единице, если заданное возмущение учитывается в ‑том сочетании и равно нулю, если не учитывается. Применяя матрицу сочетаний  усилия можно определять от единичных значений заданных возмущений, а их величины водить как компоненты матрицы . Если матрицу  принять нулевой (), то на печать будут выданы усилия от каждого возмущения в отдельности.

5. Прочие исходные данные. В расчетах на гармонические возмущения запрашивается частота заданных возмущений, масштабная жесткость и масштабная масса, число собственных чисел, интересующих пользователя программы и точность с которой определяются собственные числа. В расчетах на возмущения, изменяющиеся во времени по произвольному закону, запрашивается число интервалов, на которые разделено время действия возмущений и число отрезков, на которые разделен интервал. Запрашивается также матрица заданных возмущений. Она состоит из блоков. Число блоков рано числу интервалов, на которое разбито время действия возмущений. Компоненты ‑того столбца () каждого блока равны значению ‑того возмущения в начале, средине и конце интервала.  – число заданных возмущений. Время действия возмущений разбивается на интервалы так, чтобы на протяжении интервала на графиках возмущений не было ни перегибов, ни переломов, ни скачков. Усилия в заданной системе определяются на границах отрезков, на которые разделен интервал.

6.  Пространственные стержневые системы.   В расчетах пространственных систем стержень представляется четырьмя элементами: элементом, изгибаемом в плоскости , элементом, изгибаемом в плоскости , элементом, работающем на растяжение (сжатие), и скручиваемым элементом. Согласно принятому порядку нумерации элементов первые два имеют порядковые номера  и , а третий и четвертый -  и . Такая нумерация создает определенные визуальные неудобства при определении напряженно-деформируемого состояния стержня.

Для того, чтобы получить компактную картину усилий в стержне элемент, работающий на растяжение (сжатие), и скручиваемый элемент можно объединить в один комбинированный элемент с матрицами

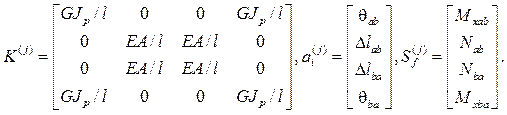
для стержня с защемленными концами;

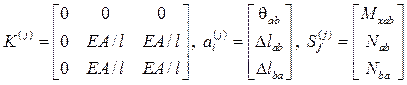
для стержня с защемленным и шарнирно опертым концами.

Матрицы  и  для комбинированных элементов, в этом случае, имеют вид

для стержня с защемленными концами.                                     

для стержня с защемленным и шарнирно опертым концами.

        В случае динамических возмущений пятые и шестые компоненты  и комбинированного элемента равны нулю.

Знак “-“ перед l – признак комбинированного элемента.

Если в расчетах нужно учесть стесненное кручение, то стержень нужно задать четырьмя элементами: два изгибаемых, один растянутый (сжатый) и элемент в состоянии стесненного кручения. Матрицы  для элемента в состоянии стесненного кручения определяются в обычном порядке, а в матрице