![]() ,
, ![]() - удвоенная площадь, ограниченная средней
линией контура,
- удвоенная площадь, ограниченная средней
линией контура, ![]() - расстояние от центра кручения
до касательной к контуру.
- расстояние от центра кручения
до касательной к контуру.
![]() - бимоменты в сечениях
- бимоменты в сечениях ![]() и
и ![]()
![]() - углы поворота сечений
- углы поворота сечений ![]() и
и ![]() относительно
оси стержня.
относительно
оси стержня. ![]() - полные крутящие моменты в
сечениях
- полные крутящие моменты в
сечениях ![]() и
и ![]() .
.
Вектор концевых усилий ![]() того элемента основной
системы от заданных возмущений равен вектору
того элемента основной
системы от заданных возмущений равен вектору
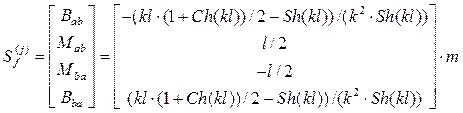 .
.
Вектор перемещений концевых сечений от единичного смещения ![]() - той связи основной системы имеет вид :
- той связи основной системы имеет вид :
![]() .
.
Вектор концевых усилий в заданной системе от заданных статических возмущений определяется суммой
![]() .
.
Влиянием сил инерции, соответствующих депланации поперечных
сечений и кручению, пренебрегаем. Поэтому концевые усилия в заданной системе от
динамических возмущений определяются так же как и от статических возмущений,но вместо
![]() подставляется вектор
подставляется вектор ![]()
Положительный угол закручивания и крутящий момент
направлены по часовой стрелке, если смотреть на сечение со стороны внешней
нормали. При определении знака бимомента и депланации , для каждого концевого
сечения выбирается правая координатная система с началом в центре кручения. Ось
![]() параллельна оси стержня и направлена к его
противоположному концу. Ось
параллельна оси стержня и направлена к его
противоположному концу. Ось ![]() параллельна стенке
условного двутавра. Положительный бимомент растягивает ближние к наблюдателю
волокна верхней полки. Наблюдатель смотрит на двутавр с положительного
направления оси
параллельна стенке
условного двутавра. Положительный бимомент растягивает ближние к наблюдателю
волокна верхней полки. Наблюдатель смотрит на двутавр с положительного
направления оси ![]() . Для наблюдателя смотрящего на
двутавр сверху (снизу) верхний (нижний) момент положительного бимомента направлен
по часовой стрелке. Согласно принятому правилу знаков бимоменты двух смежных
сечений имееют разные знаки. Положительный скручивающий момент направлен по
часовой стрелке относительно внешней нормали концевого сечения со старшим порядковым
номером.
. Для наблюдателя смотрящего на
двутавр сверху (снизу) верхний (нижний) момент положительного бимомента направлен
по часовой стрелке. Согласно принятому правилу знаков бимоменты двух смежных
сечений имееют разные знаки. Положительный скручивающий момент направлен по
часовой стрелке относительно внешней нормали концевого сечения со старшим порядковым
номером.
1.3. Тонкие плиты
Рассматривается расчет тонких плит для которых справедливы гипотезы
Кирхгова-Лява. Материал плит считается идеально упругим и ортотропным. Плита
разбивается на прямоугольники и прямоугольные треугольники. При принятии гипотезы
о нормальном элементе каждый узел имеет три степени свободы: прогиб срединной
плоскости и два угла поворота в двух взаимно перпендикулярных направлениях. За
положительный принят прогиб, направленный вниз (положительное направление оси ![]() ). Положительные углы поворота отсчитываются
против хода часовой стрелки относительно оси
). Положительные углы поворота отсчитываются
против хода часовой стрелки относительно оси ![]() и по
ходу часовой стрелки относительно оси
и по
ходу часовой стрелки относительно оси ![]() , если
смотреть в начало координат (в том и другом случаях растягиваются нижние волокна
плиты).В прямоугольном треугольнике, кроме указанных перемещений, фиксируется поворот
среднего сечения гипотенузы (точка
, если
смотреть в начало координат (в том и другом случаях растягиваются нижние волокна
плиты).В прямоугольном треугольнике, кроме указанных перемещений, фиксируется поворот
среднего сечения гипотенузы (точка ![]() на рис. 3) в перпендикулярной
ей плоскости.
на рис. 3) в перпендикулярной
ей плоскости.
Матрица – строка ![]() прогибов от единичных
смещений узловых точек определяется матричным произведением
прогибов от единичных
смещений узловых точек определяется матричным произведением
![]() .
(19)
.
(19)
![]()
для прямоугольника,
![]()
для треугольника.
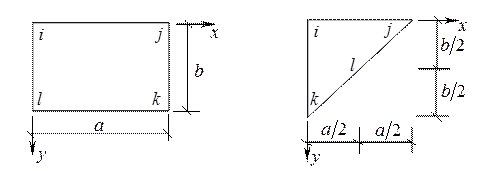
Рис. 2 Рис. 3
Матрица ![]() строится подстановкой координат
узлов, которым задаются перемещения, в
строится подстановкой координат
узлов, которым задаются перемещения, в ![]() и ее
производные.
и ее
производные.
При решении задачи узлы обходятся в последовательности: ![]() . Сначала для каждого узла фиксируется угол
поворота относительно оси
. Сначала для каждого узла фиксируется угол
поворота относительно оси ![]() -
- ![]() , затем прогиб –
, затем прогиб – ![]() и угол поворота относительно оси
и угол поворота относительно оси ![]() -
-![]() . В
треугольнике для узла
. В
треугольнике для узла ![]() фиксируется угол поворота в
плоскости нормальной прямой
фиксируется угол поворота в
плоскости нормальной прямой ![]() -
-
![]() =
=![]() .
.
![]() – угол между
прямыми
– угол между
прямыми ![]() и
и ![]() .
.
Матрицы жесткостей равны
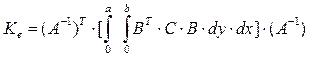 (20)
(20)
для прямоугольника,
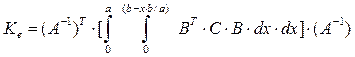 (21)
(21)
для треугольника.
Матрица ![]() – матрица деформаций,
состоящая из трех строк. Компоненты первой строки
– матрица деформаций,
состоящая из трех строк. Компоненты первой строки ![]() , второй –
, второй –
![]() , третьей –
, третьей – ![]() от
матрицы-строки
от
матрицы-строки ![]() .
.
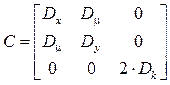 .
.
![]() ,
,
![]() .
.
Матрица реакций ![]() ‑того элемента от
смещений узлов с единичными ускорениями (матрица эквивалентных масс) равна
‑того элемента от
смещений узлов с единичными ускорениями (матрица эквивалентных масс) равна
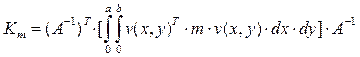 (22)
(22)
для прямоугольника,
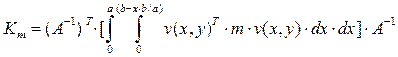 (23)
(23)
для треугольного элемента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.