Матрица L4 1; 1.00 , 9*0 , - 1.00 , 0 2; 0, -1.00 , 10*0 3; 2*0, -1.00, 9*0 4; 1.00, 9*0, -1.00, 0 5; 0, 1.00, 10*0 6; 0, 0, -1.00, 9*0 7; 3*0, 1.00, 7*0, -0.40 8; 4*0, -1.00, 7*0 9; 5*0, 1.00 ,6*0 10; 6*0, -1.00, 3*0, -1.00, 0 11; 7*0,-1.00, 4*0 12; 5*0, 1.00, 6*0 13; 6*0, 1.00, 5*0 14; 7*0, -1.00, 4*0 15; 8*0, 1,00, 4*0 16; 9*0, -1.00, 2*0
М а т р и ц а L 8 Элемент 17 1.00 (1,1), -1.00 (2,2), -1.00 (3,3), 1.00 (4,4), -1.00 (5,5), 1.00 (10,6), -1.00(11,7),-1.00(12,8),1.00(7,9),-1.00(9,10), 0.00(1,11), 0.00(4,12).
Элемент 18 1.00 (4,1), 1.00 (5,2), -1.00 (6,3), 1.00 (1,4), -1.00(3,5), 1.00 (7,6), 1.00 (8,7), -1.00(9,8), 1.00 (10,9), -1.00 (12,10).
Элемент 19 1.00(1,6), -1.00(2,7), -1.00 (3,8), 1.00 (4,9), -1.00 (6,10).
Элемент 20 1.0(4,6), 1,00 (5,7), -1.00 (6,8), 1.00 (1,9),-1.00 (3,10).
Отличные от нуля компоненты матрицы Rzm: 0.277 (1,1) 0.277 (2,2) 0.02 (3,3) 2.277 (4,4) 0.02 (5,5) 0.553 (6,6) 0.552 (7,7) 0.04 (8,8) 0.553 (9,9) 0.04 (10,10)
Компоненты верхнетреугольной части матрицы Rzz : 3.057 -0.299 -0.432 -2.928 0.421 0.943 -0.132 0.228 -1.072 -0.238 1.562 -0.057 -0.132 -0.074 0.132 0.502 0.014 0.298 0.032 0.094 0.421 -0.070 -0.228 0.014 -0.051 0.238 0.051 3.057 -0.432 -1.072 -0.298 -0.239 0.942 0.228 0.091 0.239 0.032 0.051 -0.228 -0.051 6,115 0.000 0.000 -5.857 0.000 3.123 -0.114 0.000 -0.149 0.183 0.000 -0.140 6.115 0.000 0.183
Отличные от нуля компоненты Rzk -2.000 (1,1-21) -0.400 (4,22)
Вектор собственных чисел
V = [687.79 7.89 1.54 1.11 0.83 0.20 0.17 0.14
0.06 0.04 ]![]()
Матрица первых пяти собственных векторов 1.00 0.19 0.78 1.00 0.78 0.31 0.14 0.59 0.31 0.59 0.04 0.21 1.00 0.03 0.94 -0.27 0.08 -0.37 -0.27 -0.39 -0.03 -0.07 -0.76 0.02 -0.43 -0.21 0.11 0.95 -0.20 1.00 0.10 0.04 1.00 -0.03 0.08 0.05 0.02 0.39 0.03 0.29 -0,15 -0.00 -0.13 0.00 1.00 0.02 -0.00 0.08 0.04 0.24
Матрица [ Z ], увеличенных в EJo раз перемещений узлов заданной системы
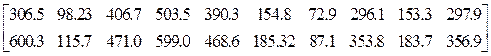
![]()
Матрицы усилий в элементах заданной системы Nxij Nxjk Nxkl Nxli Nyij Nyjk Nykl Nyli Sxy Элемент 17 -10.02 0.06 -4.00 4.29 10.08 0.10 11.08 25.33 -5.59 0.19 -1.51 -4.12 3.07 13.77 -0.25 13.05 29.36 -6,37 Элемент18 10.02 -4.29 4.00 -1.06 -10.08 -25.33 -11.08 -0.01 -5.59 - 0.19 -3.27 4.12 1.51 -13.77 -28.36 -13.05 0.25 -6.38 Элемент19 0.08 -3.88 6.10 8.29 35.51 -0.65 36.51 72.27 -5.29 0.81 -4.82 7.24 9.73 42.57 -0.81 43.68 86.32 -6.62 Элемент20 -0.08 -8.30 6.10 3.88 -35.51 -72.27 -36.51 0.65 -5.29 0.81 -9.72 -7.30 4.82 -42.57 -86.32 -43.66 0.81 -6.62
Заключение
В работе рассмотрены вопросы определения напряженно деформированного состояния линейно деформируемых систем, находящихся под действием статических и динамических возмущений.
В первой части пособия даны основные теоретические положения по определению усилий и перемещений в элементах заданной системы. Получены уравнения для определения основных неизвестных : перемещений, скоростей и ускорений узлов основной системы методом перемещений. Определены исходные данные и порядок их вода для решения задачи на ЭВМ по программе DINAM.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.