Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 9

. (10.16)

Из (10.16) имеем:

Отсюда новая действительная фундаментальная система решений может быть составлена из функци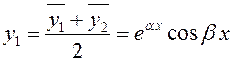й и 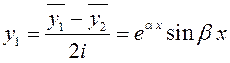, а общее решение дифференциального уравнения (10.14) тогда имеет вид:

ПРИМЕР. Найти общее решение дифференциального уравнения .

Характеристическое уравнение имеет комплексные корни .

Следовательно, ф.с.р. данного уравнения состоит из функций , а – общее решение.

Все вышесказанное можно систематизировать в виде таблицы:

Дифференциальное уравнение
Характеристическое уравнение
Корни
Ф.с.р.
Общее решение

10.3.4. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ го ПОРЯДКА

Для линейного однородного дифференциального уравнения -го порядка

, (10.17)

, , характеристическое уравнение имеет вид:

. (10.18)

Чтобы решить дифференциальное уравнение (10.17), надо решить уравнение -ой степени (10.18), которое имеет ровно корней – действительных или комплексных. По виду найденных корней выписывается ф.с.р. с учетом того, что

1) каждому простому действительному корню соответствует одно решение ;

2) каждому действительному корню кратности соответствует линейно независимых решений ;

3) каждой паре простых комплексных корней соответствует пара решений ;

4) каждой паре комплексно сопряженных корней кратности соответствует линейно независимых решений

Подчеркнем, что ф.с.р. линейного однородного дифференциального уравнения -го порядка содержит линейно независимых решений. После нахождения ф.с.р. общее решение дифференциального уравнения (10.17) запишется в виде .

ПРИМЕР. Найти общее решение дифференциальных уравнений:

а) , б) .

а) характеристическое уравнение: . Это уравнение имеет две пары действительных корней кратности

. В соответствии с п. 2) ф.с.р. состоит из функций , а общее решение имеет вид:

б) характеристическое уравнение: . Это уравнение имеет простой действительный корень и две пары комплексных корней . В соответствии с п. 1) и п. 4) составим ф.с.р.: . Отсюда общее решение имеет вид:

10.4. Методы отыскания частных решений линейных

неоднородных дифференциальных уравнений

ТЕОРЕМА 5. Пусть – некоторое решение дифференциального уравнения

, а – некоторое решение дифференциального уравнения

Тогда функция – решение дифференциального уравнения

ДОКАЗАТЕЛЬСТВО. Для доказательства достаточно подставить в уравнение:

Что и требовалось доказать.

10.4.1. МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ

Рассмотрим линейное неоднородное дифференциальное уравнение (10.11)

По теореме 4 его общее решение , где – общее решение соответствующего линейного однородного дифференциального уравнения (10.12), а – некоторое частное решение (10.11).

По теореме 3 где – ф.с.р. линейного однородного дифференциального уравнения (10.12), а – произвольные постоянные.

Идея метода вариации произвольных постоянных состоит в следующем: будем искать частное решение дифференциального уравнения (10.11) в виде, «похожем» на , именно: , где – некоторые пока неизвестные функции. Подберем эти функции так, чтобы удовлетворяло уравнению (10.11).