Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 21

ПРИМЕР.  Нетрудно проверить, что корнями многочлена третьей степени   являются числа  ,  хотя все его коэффициенты положительны.

Сформулируем (без доказательства) две теоремы, которые дают необходимые и достаточные условия отрицательности действительных частей корней многочлена. Такие теоремы называются критериями.

ТЕОРЕМА (Критерий Рауса-Гурвица). Необходимым и достаточным условием отрицательности действительных частей всех корней многочлена (12.7) является положительность всех главных диагональных миноров матрицы Рауса-Гурвица:

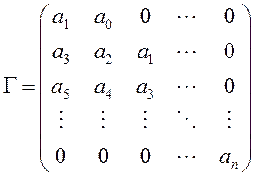                                       .                                         (12.8)

Матрица Гурвица устроена следующим образом: на ее главной диагонали стоят все коэффициенты многочлена, начиная с  ,  в столбцах стоят коэффициенты с номерами соответствующей четности, именно: в первом – нечетные, во втором – четные и т.д. Когда нужные коэффициенты заканчиваются, оставшиеся места в столбце заполняются нулями.  Таким образом, в последней строке матрицы Рауса-Гурвица только один ненулевой элемент .

Главными диагональными минорами матрицы  являются

, …, .

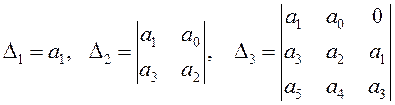Критерий Рауса-Гурвица не очень удобен для исследования корней многочлена достаточно высокой степени, так как требует вычисления, как минимум,  главных диагональных миноров матрицы  -го порядка (без первого и последнего, знак которых очевиден). Более удобным является эквивалентный ему критерий Льенара-Шипара.

ТЕОРЕМА (критерий Льенара-Шипара). Для того чтобы действительные части всех корней многочлена (12.7) были отрицательны, необходимо и достаточно, чтобы , где  – главные диагональные миноры матрицы Гурвица -го порядка.

ПРИМЕР. Проверить, являются ли отрицательными действительные части корней многочлена .

У этого многочлена  .    Необходимое условие отрицательности действительных частей корней не выполнено, значит, среди корней есть такие, у которых .

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения

а) ;     б)  .

а) Все решения неоднородного линейного дифференциального уравнения в смысле устойчивости ведут себя, как нулевое решение соответствующего однородного уравнения  . Его характеристическое уравнение имеет вид:  .

Необходимое условие отрицательности действительных частей корней этого многочлена выполнено, поэтому составим матрицу Гурвица:

.

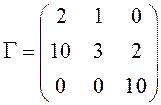По критерию Льенара-Шипара вычислим главный диагональный минор второго порядка (): 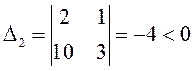.  Значит, среди корней есть числа с положительной действительной частью, а потому нулевое решение однородного дифференциального уравнения неустойчиво, что, в свою очередь, означает неустойчивость всех решений исходного неоднородного уравнения.

б) Рассуждая аналогично, составим характеристическое уравнение соответствующего однородного дифференциального уравнения:

.

Матрица Гурвица для этого многочлена – матрица четвертого порядка:

.

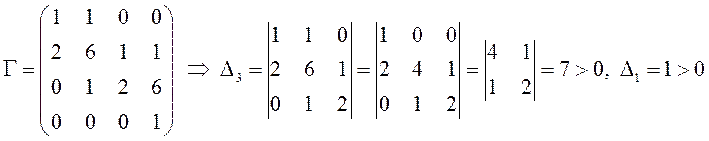Следовательно, по критерию Льенара-Шипара все, поэтому все частные решения исследуемого дифференциального уравнения асимптотически устойчивы.

12.4. Устойчивость по первому приближению

Рассмотрим автономную систему дифференциальных уравнений

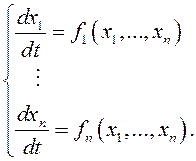                                               (12.9)

Будем полагать, что (12.9) имеет тривиальное решение, то есть , и все функции  дифференцируемы в некоторой окрестности начала координат.

В этой окрестности по определению дифференцируемой функции нескольких переменных (см.гл.6)

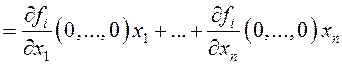
, где .

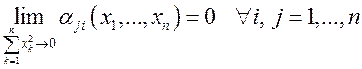Поэтому вблизи начала координат слагаемые  имеют более высокий порядок малости, чем линейные слагаемые .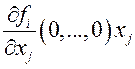

В некоторых случаях при исследовании устойчивости тривиального решения системы (12.9) нелинейными слагаемыми  правой части можно пренебречь, считая, что .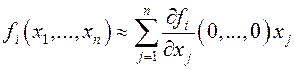

Тогда систему дифференциальных уравнений (12.9) можно заменить на близкую ей  при достаточно малых    систему

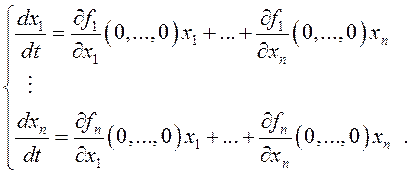
Обозначим 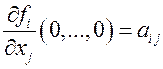 и вместо системы (12.9) рассмотрим линейную однородную систему с постоянными коэффициентами

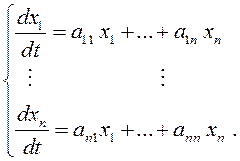                                   (12.10)

Линейная однородная система (12.10) называется системой первого приближения системы (12.9).