Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 11

. (10.25)

в) – корень кратности 2 характеристического уравнения (10.15), то есть, . Как было показано ранее, из теоремы Виета следует, что в этом случае . Тогда в левой части (10.24) стоит многочлен степени , и чтобы (10.24) было тождеством, частное решение следует искать в виде произведения и многочлена -ой степени без двух последних слагаемых, которые при вычислении пропадают.

Таким образом,

. (10.26)

ПРИМЕР. Найти вид частного решения дифференциального уравнения в случаях, когда

а) , б) , в) .

Составим и решим характеристическое уравнение однородного дифференциального уравнения : .

а) Специальная правая часть I типа в общем случае имеет вид .В данном случае а не является корнем характеристического уравнения. В соответствии с (10.23) , где – неопределенные коэффициенты.

б) В этом случае а – простой корень характеристического уравнения, поэтому частное решение имеет вид (10.25):

, где А и В – неопределенные коэффициенты.

в) Эта правая часть также имеет специальный вид: 4 – многочлен нулевой степени, а среди корней не встречается. Отсюда , где – неопределенный коэффициент.

ПРИМЕР. Найти вид частного решения дифференциального уравнения в случаях, когда

а) , б) .

Характеристическое уравнение: .

а) корнем не является, поэтому в соответствии с (10.23)

б) – корень кратности 2, поэтому частное решение имеет вид (10.26):

ПРИМЕР. Найти общее решение дифференциального уравнения .

Выше были найдены корни характеристического уравнения, поэтому по теореме о структуре общего решения линейного однородного дифференциального уравнения .

Частное решение этого дифференциального уравнения имеет вид . Чтобы найти коэффициенты , подставим эту функцию в уравнение: ,

Приравнивая коэффициенты при одинаковых степенях слева и справа, получим:

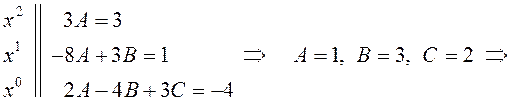
Таким образом, по теореме о структуре общего решения линейного неоднородного дифференциального уравнения является искомым общим решением.

Рассмотрим теперь правую часть специального вида II типа

где многочлены соответственно -ой и -ой степеней.

По формуле Эйлера (10.16): ,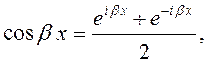

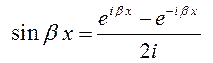отсюда

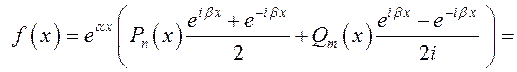
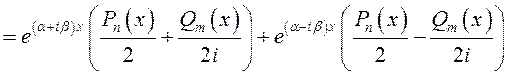Заметим, что степень многочленов 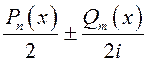равна .

После такого преобразования правой части рассмотрение случая II сводится уже к рассмотренному случаю I, именно:

а) если не является корнем характеристического уравнения (10.15), то

, (10.27)

где – многочлены степени с неопределенными коэффициентами;

б) если – корень характеристического уравнения и , то

. (10.28)

ПРИМЕР. Найти вид частного решения дифференциального уравнения в случаях, когда

а) , б) .

Характеристическое уравнение имеет корни .

а) Специальная правая часть II типа в общем виде имеет вид

В данном случае , поэтому . Комплексное число корнем не является, а .

Поэтому частное решение запишется по формуле (10.27):

, где А, В, С, D – неопределенные коэффициенты.

б) В этом случае . Комплексное число корнем не является, поэтому и здесь частное решение имеет вид (10.27):

, где А, В – коэффициенты, которые надо определить.

Следует обратить внимание на то, что, несмотря на отсутствие в правой части уравнения , частное решение ищется как линейная комбинация обеих функций и .