12.1. Понятие устойчивости по Ляпунову
Рассмотрим нормальную систему дифференциальных уравнений:
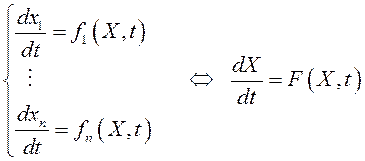 . (12.1)
. (12.1)
Пусть
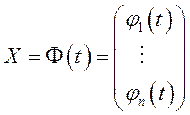 – решение системы (12.1), соответствующее
начальным условиям
– решение системы (12.1), соответствующее
начальным условиям ![]() , или
, или 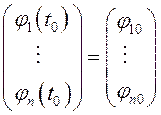 .
.
Кроме
того, 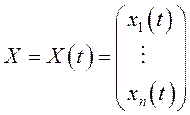 – решение системы (12.1), соответствующее
измененным начальным условиям
– решение системы (12.1), соответствующее
измененным начальным условиям ![]() , или
, или 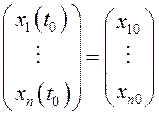 .
.
ОПРЕДЕЛЕНИЕ.
Решение системы (12.1) ![]() называется устойчивым по
Ляпунову, если для любого
называется устойчивым по
Ляпунову, если для любого ![]() существует
существует ![]() такое, что из совокупности неравенств
такое, что из совокупности неравенств ![]() следуют неравенства
следуют неравенства ![]() .
.
Из определения следует, что если ![]() – устойчивое решение, то всякое
решение, достаточно близкое к нему в начальный момент
– устойчивое решение, то всякое
решение, достаточно близкое к нему в начальный момент ![]() ,
остается близким к нему с ростом
,
остается близким к нему с ростом ![]() .
.
ОПРЕДЕЛЕНИЕ.
Решение системы (12.1) ![]() называется асимптотически
устойчивым по Ляпунову, если существует
называется асимптотически
устойчивым по Ляпунову, если существует ![]() такое,
что из совокупности неравенств
такое,
что из совокупности неравенств ![]() следует, что
следует, что ![]()
![]() .
.
Из определения следует, что всякое решение,
достаточно близкое к ![]() в начальный момент
в начальный момент ![]() , неограниченно сближается с ним с ростом
, неограниченно сближается с ним с ростом
![]() .
.
ПРИМЕР.
Рассмотрим дифференциальное уравнение первого порядка 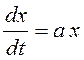 ,
где
,
где ![]() – параметр. Очевидно, что это уравнение
имеет тривиальное решение
– параметр. Очевидно, что это уравнение
имеет тривиальное решение ![]() , удовлетворяющее при
любом
, удовлетворяющее при
любом ![]() начальному условию
начальному условию ![]()
Исследуем
на устойчивость это решение. Для этого зададим другое начальное условие ![]() и найдем решение, которое ему
удовлетворяет.
и найдем решение, которое ему
удовлетворяет.
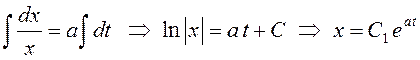 – общее решение уравнения.
– общее решение уравнения.
![]() – искомое частное решение.
– искомое частное решение.
Отсюда ![]() .
.
1)
Пусть ![]()
![]() , поэтому каким бы близким к нулю ни было
значение
, поэтому каким бы близким к нулю ни было
значение ![]() ,
, ![]() неограниченно
возрастает, то есть найденное решение неограниченно удаляется от решения
неограниченно
возрастает, то есть найденное решение неограниченно удаляется от решения ![]() . А это по определению означает, что при
. А это по определению означает, что при ![]() нулевое решение свойством устойчивости не
обладает, или является неустойчивым (рис.5).
нулевое решение свойством устойчивости не
обладает, или является неустойчивым (рис.5).
|
2)
Пусть ![]() при
всех
при
всех ![]() , значит
, значит ![]() .
Зададим
.
Зададим ![]() . Тогда при
. Тогда при ![]() получим,
что если
получим,
что если ![]() , то
, то ![]() .
Определение устойчивости выполнено, поэтому при
.
Определение устойчивости выполнено, поэтому при ![]() нулевое
решение устойчиво по Ляпунову (рис.6, 7).
нулевое
решение устойчиво по Ляпунову (рис.6, 7).
Заметим, что если ![]() , то
, то ![]() , то есть в этом случае нулевое решение
асимптотически устойчиво (рис.7).
, то есть в этом случае нулевое решение
асимптотически устойчиво (рис.7).
|
|
ОПРЕДЕЛЕНИЕ.
Решение системы (12.1) ![]() называется асимптотически
устойчивым в целом, если
называется асимптотически
устойчивым в целом, если ![]() где
где ![]() решение, определяемое любыми
начальными условиями, а не только значениями, близкими к начальным значениям
решение, определяемое любыми
начальными условиями, а не только значениями, близкими к начальным значениям ![]() ,
,![]() .
.
Как было показано выше, при ![]() нулевое решение д.у.
нулевое решение д.у. 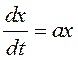 асимптотически устойчиво в целом.
асимптотически устойчиво в целом.
Рассмотрим систему уравнений (12.1). Каждому решению (12.1) соответствует
интегральная кривая 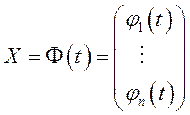 , или траектория. Если
эта система имеет не зависящее от
, или траектория. Если
эта система имеет не зависящее от ![]() решение
решение 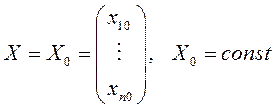 , то соответствующая траектория будет
точкой. Она называется точкой покоя системы (12.1), или ее положением
равновесия. В частности, тривиальное решение
, то соответствующая траектория будет
точкой. Она называется точкой покоя системы (12.1), или ее положением
равновесия. В частности, тривиальное решение 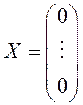 называется
точкой покоя этой системы, расположенной в начале координат (она
существует, лишь если
называется
точкой покоя этой системы, расположенной в начале координат (она
существует, лишь если ![]() ).
).
Сформулируем определение устойчивой точки покоя, расположенной в начале координат.
ОПРЕДЕЛЕНИЕ.
Тривиальное решение системы (12.1) называется устойчивым по Ляпунову,
если для любого ![]() существует
существует ![]() такое, что из совокупности неравенств
такое, что из совокупности неравенств ![]() следуют неравенства
следуют неравенства ![]() .
.
Такому определению можно дать другую, эквивалентную формулировку.
ОПРЕДЕЛЕНИЕ.
Точка покоя, расположенная в начале координат, называется устойчивой по
Ляпунову, если для любого ![]() существует
существует ![]() такое, что из неравенства
такое, что из неравенства 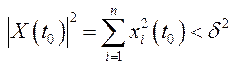 следует, что
следует, что
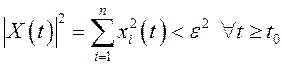 .
.
|
Геометрически
это означает, что если тривиальное решение устойчиво, то всякая траектория,
определяемая начальной точкой |
ОПРЕДЕЛЕНИЕ.
Тривиальное решение системы (12.1) называется асимптотически устойчивым,
если существует ![]() такое, что из совокупности
неравенств
такое, что из совокупности
неравенств ![]() следует, что
следует, что ![]() , или,
другими словами, если из неравенства
, или,
другими словами, если из неравенства 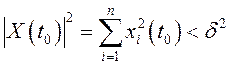 следует,
что
следует,
что
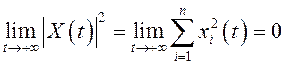 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.