Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 18

Геометрическая иллюстрация этого определения – рис. 9: если тривиальное решение асимптотически устойчиво, то любая траектория, которая определяется начальной точкой в круге радиуса , не только не выйдет из этого круга, но и будет стремиться к его центру .

Оказывается, что исследование на устойчивость любого частного решения системы (12.1) можно заменить исследованием устойчивости тривиального решения некоторой другой системы.  Покажем это.

Пусть  – исследуемое решение. Введем новую переменную . Если решение  устойчиво, то любое решение , близкое к нему в начальный момент , остается близким к нему и при . Отсюда следует, что если при   близко к началу координат, то  не удаляется от  и с ростом .

Выясним, какой системе уравнений удовлетворяет функция , если  удовлетворяет (12.1):

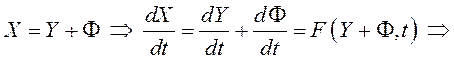
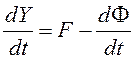                     .                                                  (12.2)

Система (12.2)  имеет тривиальное решение . Если оно устойчиво, то устойчиво любое частное решение системы (12.1).

Рассмотрим линейную неоднородную систему

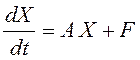                                                                      (12.3)

и соответствующую ей однородную систему линейных дифференциальных уравнений

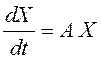                      .                                                   (12.4)

Исследуем на устойчивость частное решение системы (12.3) . Пусть   – это отклонение точек на произвольной траектории  от соответствующих точек исследуемой траектории . Такое отклонение называется возмущением.

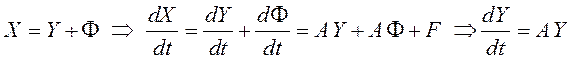, так как   удовлетворяет (12.3).

Таким образом, если решение  неоднородной системы (12.3) устойчиво, то устойчиво и тривиальное решение соответствующей однородной системы (12.4) и наоборот: из устойчивости нулевого решения однородной системы (12.4) следует устойчивость решения   неоднородной системы (12.3).

Итак, все частные решения неоднородной системы (12.3) в смысле устойчивости ведут себя так же, как тривиальное решение соответствующей однородной системы (12.4). Поэтому исследование устойчивости произвольного решения системы (12.3) можно заменить исследованием устойчивости точки покоя, расположенной в начале координат, однородной системы (12.4).

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения  .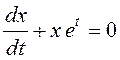

Это линейное однородное уравнение, оно имеет тривиальное решение , которое удовлетворяет начальному условию .

Исследуем устойчивость этого решения. Изменим начальное условие: – и найдем соответствующее ему решение.

.

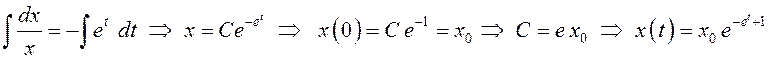Так как  , то тривиальное решение асимптотически устойчиво в целом, а это означает, что асимптотически устойчивы в целом и все частные решения данного дифференциального уравнения.

ПРИМЕР. Исследовать на устойчивость решения системы дифференциальных уравнений  .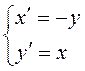

Сведем систему к одному дифференциальному уравнению 2-го порядка: из второго уравнения получаем

.

Тогда .

Итак, 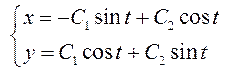 – общее решение системы.

Очевидно, что данная система имеет точку покоя, расположенную в начале координат. Такое решение удовлетворяет условию . Чтобы исследовать  его устойчивость, рассмотрим произвольное решение, определяемое начальным условием 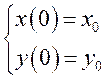 . Оно имеет вид .

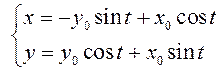При достаточно малых значениях  значения  также будут достаточно малы, потому что . А это означает, что тривиальное решение и вместе с ним все частные решения данной системы устойчивы, хотя асимптотической устойчивости нет.

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения .

Найдем общее решение: характеристическое уравнение имеет вид

.

Отсюда следует, что нулевое решение этого дифференциального уравнения  асимптотически устойчиво в целом, а это значит, что асимптотически устойчивы в целом не только все частные решения данного однородного дифференциального уравнения, но и все частные решения неоднородного уравнения .

ПРИМЕР. Исследовать на устойчивость решения дифференциального уравнения .