Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 2

Разложив вектор  на вертикальную и горизонтальную составляющие, получим уравнения равновесия:

   .

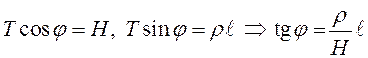
Пусть уравнение нити имеет вид , тогда .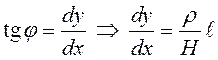

Как известно (см. гл.8), 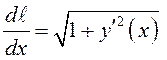, поэтому .

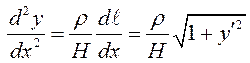Таким образом, получено дифференциальное уравнение цепной линии:

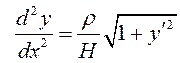                         .                                           (10.2)

Это уравнение связывает первую и вторую производные неизвестной функции. Заметим, что искомое решение удовлетворяет условиям  (рис.1).

Как показывают эти примеры, дифференциальное уравнение может содержать первую, вторую, а также производные более высоких порядков неизвестной функции.

ОПРЕДЕЛЕНИЕ. Уравнение, которое связывает неизвестную функцию (или функции), ее производные и независимую переменную (или переменные), называется дифференциальным уравнением. Если неизвестная функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – уравнением с частными производными.

ОПРЕДЕЛЕНИЕ. Порядком дифференциального уравнения называется старший из порядков входящих в него производных.

ПРИМЕР. Уравнение (10.1) является обыкновенным дифференциальным уравнением первого порядка, (10.2) – обыкновенным дифференциальным уравнением второго порядка.

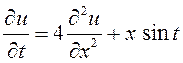 – уравнение с частными производными второго порядка.

ОПРЕДЕЛЕНИЕ. Решением дифференциального уравнения называется функция, подстановка которой в уравнение обращает его в тождество. Если решение найдено в неявном виде, оно называется интегралом данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.

ПРИМЕР. 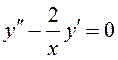 – дифференциальное уравнение второго порядка. Легко проверить, что, например,  является его решением. Также является решением  .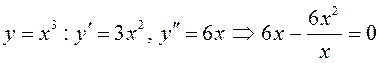 

Функция  этому уравнению не удовлетворяет, значит, решением не является.

Перейдем к изучению дифференциальных уравнений первого порядка.

10.2. Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка связывает независимую переменную, неизвестную функцию и  ее первую производную, то есть имеет вид .

Уравнение вида                             

                                                  (10.3)

называется уравнением, разрешенным относительно производной.

Так как 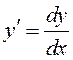, то (10.3) можно переписать в виде .      В общем виде дифференциальное уравнение первого порядка может быть записано и таким образом:

.

ПРИМЕР.  – дифференциальное уравнение первого порядка. Перепишем его: 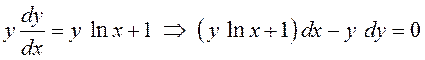. Наоборот, уравнение первого порядка  может быть после деления обеих его частей на  записано так:   .

Рассмотрим дифференциальное уравнение .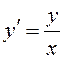          

Легко проверить, что   и вообще  – решения этого дифференциального уравнения. Каждому из этих решений соответствует интегральная кривая: прямая линия, проходящая через начало координат (рис. 2).   Если задать произвольную точку плоскости , то через нее проходит интегральная кривая , а через точки  не проходит ни одной интегральной кривой (рис. 2).

Таким образом, можно сделать следующий вывод:

1)  данное дифференциальное уравнение имеет бесконечное множество решений,

2)  через любую точку плоскости, кроме принадлежащих оси , проходит единственная интегральная кривая,

3)  через точки на оси  либо не проходит ни одной интегральной кривой , либо проходит бесконечно много интегральных кривых (начало координат).

Этот вывод является иллюстрацией следующей теоремы.

ТЕОРЕМА Коши (о существовании и единственности решения дифференциального уравнения первого порядка). Пусть функция  – непрерывна вместе с производной  в некоторой плоской области . Тогда для любой точки  существует, причем единственное, решение дифференциального уравнения (10.3), удовлетворяющее начальному условию .

Без доказательства.

Задача отыскания решения дифференциального уравнения , удовлетворяющего начальному условию , называется задачей Коши.