ТЕОРЕМА (о
структуре общего решения линейной однородной системы дифференциальных
уравнений). Пусть ![]() – линейно независимые решения системы
(11.3) с непрерывными коэффициентами
– линейно независимые решения системы
(11.3) с непрерывными коэффициентами ![]() Тогда ее общее
решение имеет вид:
Тогда ее общее
решение имеет вид: ![]() , где
, где ![]() –
произвольные постоянные.
–
произвольные постоянные.
ДОКАЗАТЕЛЬСТВО.
По теореме о линейной комбинации решений вектор-функция ![]() является решением системы (11.3).
является решением системы (11.3).
Зададим начальное условие, удовлетворяющее условиям теоремы Коши
![]()
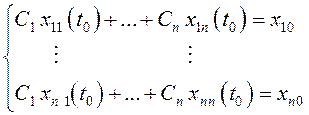 – система линейных уравнений, основной определитель
которой
– система линейных уравнений, основной определитель
которой ![]() , так по условию решения
, так по условию решения ![]() линейно независимы. Значит, система имеет
единственное решение
линейно независимы. Значит, система имеет
единственное решение ![]() , а
, а ![]() –
решение (11.3), удовлетворяющее поставленному начальному условию.
–
решение (11.3), удовлетворяющее поставленному начальному условию.
Что и требовалось доказать.
ТЕОРЕМА (о
структуре общего решения линейной неоднородной системы дифференциальных
уравнений). Пусть ![]() – некоторое частное решение
линейной неоднородной системы дифференциальных уравнений (11.2), а
– некоторое частное решение
линейной неоднородной системы дифференциальных уравнений (11.2), а
![]() – общее решение
соответствующей однородной системы (11.3). Тогда общее решение системы (11.2)
имеет вид:
– общее решение
соответствующей однородной системы (11.3). Тогда общее решение системы (11.2)
имеет вид: ![]() .
.
Доказать самостоятельно.
11.2. Решение систем линейных однородных дифференциальных
уравнений с постоянными коэффициентами
Рассмотрим линейную однородную систему дифференциальных уравнений с постоянными коэффициентами:
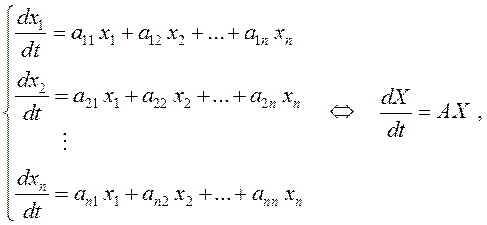 (11.4)
(11.4)
где
![]() .
.
Будем
искать решение (11.4) в виде ![]() , или
, или 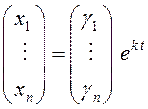 , где
, где 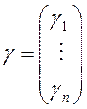 –
некоторый постоянный вектор. Очевидно,
–
некоторый постоянный вектор. Очевидно, 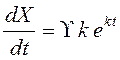 , поэтому
после подстановки
, поэтому
после подстановки ![]() в (11.4) получим:
в (11.4) получим:
![]() , где
, где
![]() – единичная матрица
– единичная матрица ![]() -го порядка. Запишем последнее равенство в
виде системы линейных алгебраических уравнений относительно неизвестных
-го порядка. Запишем последнее равенство в
виде системы линейных алгебраических уравнений относительно неизвестных ![]() :
:
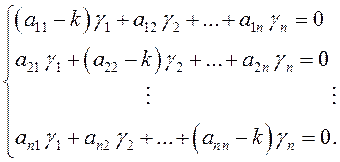 (11.5)
(11.5)
Как известно (см.гл.1), однородная система линейных алгебраических уравнений имеет нетривиальное решение тогда и только тогда, когда ее определитель равен нулю, то есть
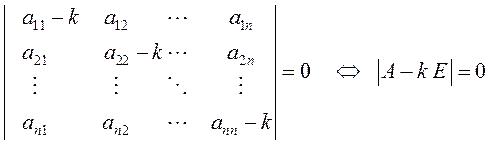 . (11.6)
. (11.6)
Уравнение (11.6) называется характеристическим уравнением
матрицы ![]() . Оно является уравнением
. Оно является уравнением ![]() -ой степени относительно
-ой степени относительно ![]() и потому имеет ровно
и потому имеет ровно ![]() корней – действительных или комплексных.
корней – действительных или комплексных.
Корни характеристического уравнения (11.6) называются собственными
значениями матрицы ![]() .
.
Решим (11.6) и найдем все собственные значения матрицы А.
Подставляя каждое из них в (11.5), будем получать
систему линейных однородных уравнений с нулевым определителем. Любое
нетривиальное решение этой системы 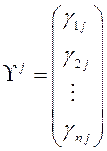 называется собственным
вектором матрицы
называется собственным
вектором матрицы ![]() , соответствующим собственному
значению
, соответствующим собственному
значению ![]() .
.
Можно показать, что если уравнение (11.6) не имеет
кратных корней, то существует ![]() линейно независимых
собственных векторов
линейно независимых
собственных векторов ![]() , то есть таких векторов, ни один
из которых не выражается через другие с помощью линейной комбинации.
, то есть таких векторов, ни один
из которых не выражается через другие с помощью линейной комбинации.
Найдя для каждого собственного значения матрицы ![]() собственный вектор, получим
собственный вектор, получим ![]() линейно независимых решений системы
(11.4):
линейно независимых решений системы
(11.4): ![]() . Тогда по теореме о структуре общего
решения линейной однородной системы общее решение запишется в виде
. Тогда по теореме о структуре общего
решения линейной однородной системы общее решение запишется в виде ![]() .
.
Решение системы (11.4) зависит от характера корней характеристического уравнения (11.6): они могут быть действительными или комплексными, простыми или кратными.
Рассмотрим на примерах всевозможные случаи.
1) Все корни (11.6) действительны и различны.
ПРИМЕР. Решить систему дифференциальных уравнений:
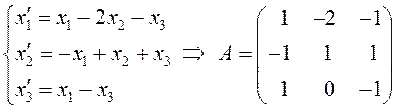 .
.
Составим
характеристическое уравнение (11.6) ![]() :
:
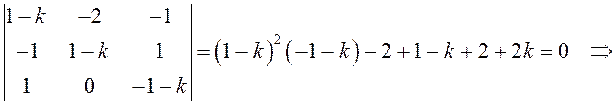
![]() – собственные значения матрицы
– собственные значения матрицы ![]() .
.
Найдем собственные векторы.
а) ![]() . Подставим это значение
в (11.5):
. Подставим это значение
в (11.5):
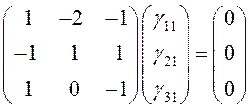 – векторная запись системы (11.5), или
– векторная запись системы (11.5), или
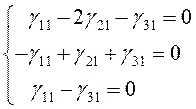 – система трех линейных уравнений с
определителем
– система трех линейных уравнений с
определителем ![]() . Заметим, что ранг основной
матрицы этой системы равен 2, поэтому система имеет одну свободную переменную.
Выберем любые два уравнения, зададим одну из переменных произвольно (например,
. Заметим, что ранг основной
матрицы этой системы равен 2, поэтому система имеет одну свободную переменную.
Выберем любые два уравнения, зададим одну из переменных произвольно (например, ![]() ) и найдем частное решение:
) и найдем частное решение:
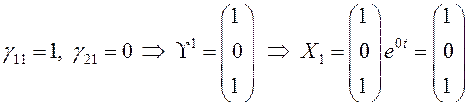 .
.
ЗАМЕЧАНИЕ.
Так как основной определитель ![]() системы (11.5) равен
нулю, то алгебраические дополнения элементов любой ее строки являются частными
решениями:
системы (11.5) равен
нулю, то алгебраические дополнения элементов любой ее строки являются частными
решениями: ![]() (напомним, что
(напомним, что ![]() , где
, где ![]() – дополнительный минор). Действительно,
полагая, например,
– дополнительный минор). Действительно,
полагая, например, ![]() , получим:
, получим:
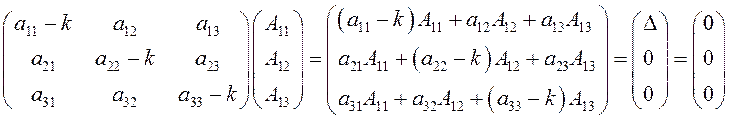
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.