Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 23

на траектории до начала координат не увеличивается, то есть все траектории, определяемые частными решениями, близкими к в начальный момент, остаются близкими к началу координат и с ростом . Это по определению означает, что тривиальное решение устойчиво.

Если 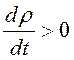, то расстояние с ростом  увеличивается, следовательно, нулевое решение неустойчиво.

Функция 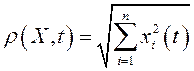 в этих рассуждениях может быть заменена на более удобную в вычислениях функцию .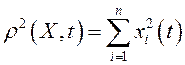

ПРИМЕР. Исследовать на устойчивость нулевое решение системы дифференциальных уравнений .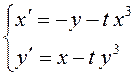

Пусть . Найдем производную этой функции вдоль траекторий системы:

.

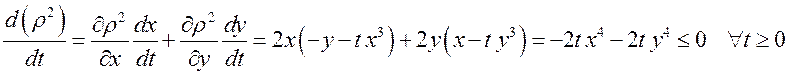Таким образом,  – невозрастающая функция, то есть точки на произвольной траектории не удаляются от начала координат, поэтому тривиальное решение системы устойчиво, а, значит, устойчивы все решения этой системы.

Отметим, что из неравенства 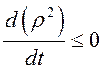 следует, что  – монотонная функция. Но точка покоя может быть устойчивой и при немонотонном приближении к ней траекторий, соответствующих произвольным решениям (центр или устойчивый фокус (рис. 13, 14)). Поэтому в качестве функций, с помощью которых исследуется устойчивость, Ляпунов рассмотрел функции, некоторые свойства которых схожи со свойствами расстояния, но сами они расстояниями не являются.

ОПРЕДЕЛЕНИЕ. Производной функции  в силу системы (12.1) называется полная производная .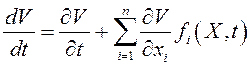

Рассмотрим автономную систему

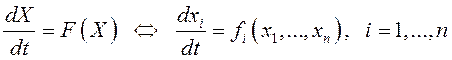 .                          (12.12)

Будем считать, что для такой  системы функция  не зависит от времени и ее производная в силу системы (12.12) имеет вид:   .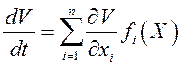

ОПРЕДЕЛЕНИЕ. Функция  называется положительно (отрицательно) определенной в некоторой -окрестности начала координат, если всюду в этой окрестности  и только . Положительно или отрицательно определенные функции называются знакоопределенными.

Напомним, что -окрестностью начала координат называется множество точек, определяемое неравенством 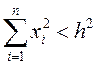. Если , то это круг радиуса  с центром в начале координат, если  – то шар радиуса .

ПРИМЕРЫ. а)  всюду, кроме начала координат, а . Отсюда  – положительно определенная функция.

б) , причем 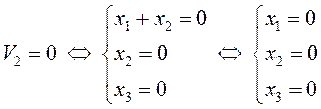. Значит, по определению  – положительно определенная функция.

в) .

Но 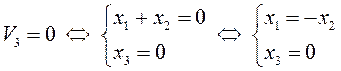, поэтому  положительно определенной функцией не является: она равна нулю не только в начале координат.

ОПРЕДЕЛЕНИЕ. Функция  называется неотрицательной (неположительной) в некоторой -окрестности начала координат, если всюду в этой окрестности  , причем   не только при . Неотрицательные или неположительные функции называются знакопостоянными.

ПРИМЕР. Функция  является по определению неотрицательной.

ПРИМЕР. , .

По определению функция    не является  ни  знакоопределенной,          ни знакопостоянной.

ОПРЕДЕЛЕНИЕ. Функция  называется функцией Ляпунова автономной системы (12.12), если

1)   дифференцируема в некоторой окрестности начала координат;

2)   положительно определена (отрицательно определена) в этой окрестности;

3)  ее производная в силу системы (12.12) 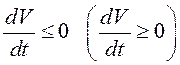 всюду в этой окрестности.

Рассмотрим систему (12.12) и будем считать, что она имеет тривиальное решение , то есть .

ТЕОРЕМА (Ляпунова об устойчивости). Пусть существует дифференцируемая функция , знакоопределенная в некоторой окрестности начала координат, производная которой в силу системы (12.12) знакопостоянна в этой окрестности и противоположного с  знака или тождественно равная нулю. Тогда тривиальное решение системы (12.12) устойчиво.

ДОКАЗАТЕЛЬСТВО. Пусть функция  дифференцируема и положительно определена в некоторой -окрестности начала координат, а ее производная в силу системы (12.12) 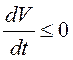   или 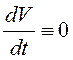 . Зададим

и пусть  – граница -окрестности начала координат (рис. 22). Из  дифференцируемости  следует ее непрерывность как внутри -окрестности, так и на ее границе . Граница  – ограниченное и замкнутое множество, поэтому непрерывная функция  достигает на ней своих наибольшего и наименьшего значений. Обозначим  – наименьшее значение   на  .  Отметим,  что,  так  как   положительно определена, то . Функция  непрерывна в -окрестности начала координат,  , а на  имеет место неравенство . Поэтому существует такая -окрестность (), во всех точках которой .