Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 8

  или    ,  .

ОПРЕДЕЛЕНИЕ. Совокупность  линейно независимых решений линейного однородного дифференциального уравнения (10.12) называется его фундаментальной системой решений (ф.с.р.).

ПРИМЕР. Фундаментальную систему решений (ф.с.р.) уравнения  образуют, например, функции , или функции .

ТЕОРЕМА 4 (о структуре общего решения линейного неоднородного  дифференциального уравнения). Пусть  – некоторое частное решение линейного неоднородного дифференциального уравнения (10.11) с непрерывными коэффициентами , а  – общее решение соответствующего однородного дифференциального уравнения  (10.12). Тогда общее решение дифференциального уравнения (10.11) имеет вид: .

ДОКАЗАТЕЛЬСТВО. Покажем, что  – решение дифференциального уравнения (10.11). Подставим эту функцию в уравнение:  

.

Покажем, что это решение – общее. Зададим произвольные начальные условия ,  удовлетворяющие  условиям  теоремы  Коши.

По теореме 3  , где решения  дифференциального уравнения (10.12) образуют ф.с.р. Тогда для определения постоянных  получим систему линейных алгебраических уравнений 

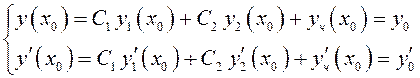
или 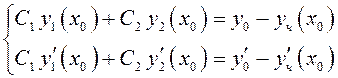                                 , основной определитель которой  по теореме 2. 

Значит, эта система имеет единственное решение , а функция   – решение дифференциального уравнения (10.11), удовлетворяющее заданным начальным условиям.

Таким образом, по определению  – общее решение дифференциального уравнения (10.11).

Что и требовалось доказать.

10.3.3. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Рассмотрим линейное однородное уравнение второго порядка

                              ,                                       (10.14)

где  , .

Будем искать решение дифференциального уравнения (10.14) в виде . Подставим эту функцию в уравнение:

                                                      .                                       (10.15)

Если  удовлетворяет уравнению (10.15), то функция  является решением дифференциального уравнения (10.14).

Уравнение (10.15) называется характеристическим уравнением линейного однородного дифференциального уравнения (10.14).

Решение дифференциального уравнения (10.14) будет зависеть от характера корней квадратного уравнения (10.15). Как всякое квадратное уравнение, оно может иметь либо пару действительных различных корней , либо совпадающие (двукратные) корни , либо пару комплексно-сопряженных корней .

Рассмотрим всевозможные случаи.

1) Пусть характеристическое уравнение имеет различные действительные корни . Тогда  – решения дифференциального уравнения (10.14), причем 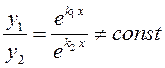. Следовательно,  линейно независимы, а потому образуют ф.с.р. По теореме 3 общее решение (10.14) в этом случае имеет вид

.

ПРИМЕР. Найти общее решение дифференциального уравнения .

Составим и решим характеристическое уравнение:

 – ф.с.р.

Тогда   – общее решение этого дифференциального уравнения.

2) Пусть характеристическое уравнение имеет действительные равные корни . Тогда  – решение дифференциального уравнения (10.14). Покажем, что в качестве второго решения, линейно независимого с этим, можно взять функцию .

Подставим эту функцию в уравнение:

  

, где  – двукратный корень уравнения (10.15). По теореме Виета 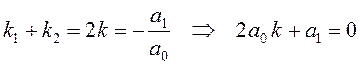, поэтому    удовлетворяет уравнению (10.14). Кроме того, 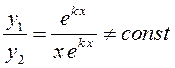, то есть  образуют ф.с.р.,          и общее решение дифференциального уравнения (10.14) в этом случае          имеет вид:

.

ПРИМЕР. Найти общее решение дифференциального уравнения .

Характеристическое уравнение

.

Отсюда ф.с.р. состоит из функций  и общее решение имеет вид .

3) Пусть характеристическое уравнение (10.15) имеет комплексные  корни

. Так как , то решения    линейно независимы, значит, образуют ф.с.р. Но по теореме 1 при любых   – решение (10.14),  поэтому  подберем  постоянные        и  так, чтобы получить пару действительных линейно независимых решений уравнения. Воспользуемся для этого формулой Эйлера (она будет доказана позже в гл.13)