Заметим,
что из равенства 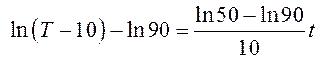 следует, что температура тела
изменяется по закону
следует, что температура тела
изменяется по закону 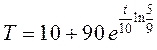 , или
, или 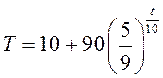 – эта
функция является решением задачи Коши, поставленной в рассмотренном примере.
– эта
функция является решением задачи Коши, поставленной в рассмотренном примере.
10.2.2. ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение первого порядка называется однородным, если его можно привести к виду
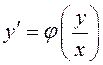 .
(10.5)
.
(10.5)
ПРИМЕРЫ. а) 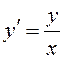 – однородное дифференциальное
уравнение первого порядка (это уравнение также является дифференциальным
уравнением с разделяющимися переменными);
– однородное дифференциальное
уравнение первого порядка (это уравнение также является дифференциальным
уравнением с разделяющимися переменными);
б) 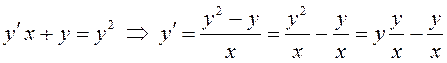 – не является однородным,
так как не может быть приведено к виду (10.5);
– не является однородным,
так как не может быть приведено к виду (10.5);
в) ![]() . Чтобы убедиться в
том, что это однородное дифференциальное уравнение, разделим обе его части на
. Чтобы убедиться в
том, что это однородное дифференциальное уравнение, разделим обе его части на ![]() :
:
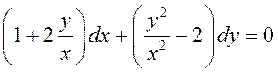
![]()
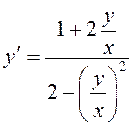 .
.
Теперь стало очевидным, что данное уравнение приводится к виду (10.5), то есть является однородным.
ОПРЕДЕЛЕНИЕ.
Многочлен ![]() -ой степени относительно двух переменных
-ой степени относительно двух переменных ![]() называется однородным многочленом,
если сумма показателей степеней во всех его одночленах одинакова и равна
называется однородным многочленом,
если сумма показателей степеней во всех его одночленах одинакова и равна ![]() .
.
ПРИМЕРЫ. а) ![]() – однородный многочлен
первой степени;
– однородный многочлен
первой степени;
б) ![]() – однородный многочлен
третьей степени;
– однородный многочлен
третьей степени;
в) ![]() – однородные
многочлены второй степени;
– однородные
многочлены второй степени;
г) ![]() – не является однородным
многочленом.
– не является однородным
многочленом.
Уравнения вида ![]() , или
, или 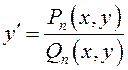 , где
, где ![]()
![]() – однородные многочлены
– однородные многочлены
![]() -ой степени, являются однородными дифференциальными
уравнениями первого порядка.
-ой степени, являются однородными дифференциальными
уравнениями первого порядка.
Однородное дифференциальное уравнение первого порядка сводится
к уравнению с разделяющимися переменными в результате замены переменной
по формуле: 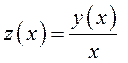 . Действительно, так как
. Действительно, так как ![]() , то
, то ![]() ,
поэтому после выполнения подстановки уравнение (10.5) примет вид
,
поэтому после выполнения подстановки уравнение (10.5) примет вид ![]() , а дифференциальное уравнение
, а дифференциальное уравнение ![]() является уравнением с разделяющимися
переменными.
является уравнением с разделяющимися
переменными.
ПРИМЕР.
Решить задачу Коши 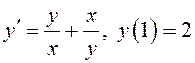 .
.
Данное дифференциальное уравнение является однородным,
поэтому сделаем замену переменной 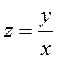 . Тогда имеем:
. Тогда имеем: 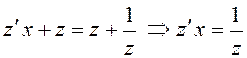 – уравнение с разделяющимися переменными. Решим
его:
– уравнение с разделяющимися переменными. Решим
его:
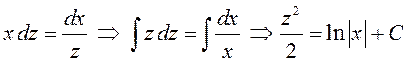 .
.
Возвращаясь к «старым»
переменным, получим общий интеграл 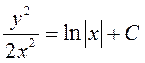 .
.
Найдем решение, удовлетворяющее
начальному условию ![]() :
:
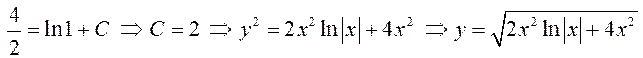 – искомое частное
решение.
– искомое частное
решение.
Заметим, что если задать начальное
условие ![]() , то соответствующее частное решение будет
иметь вид
, то соответствующее частное решение будет
иметь вид ![]() .
.
10.2.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение первого порядка называется линейным, если неизвестная функция и ее производная входят в него линейно, то есть в первой степени. Такое уравнение имеет вид
![]() .
(10.6)
.
(10.6)
Если ![]() , то дифференциальное уравнение
, то дифференциальное уравнение
![]() называется линейным однородным дифференциальным
уравнением первого порядка (оно является также дифференциальным уравнением с
разделяющимися переменными). Если
называется линейным однородным дифференциальным
уравнением первого порядка (оно является также дифференциальным уравнением с
разделяющимися переменными). Если ![]() , то уравнение
называется линейным неоднородным.
, то уравнение
называется линейным неоднородным.
ПРИМЕРЫ.
а) 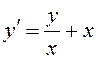 – линейное неоднородное дифференциальное
уравнение;
– линейное неоднородное дифференциальное
уравнение;
б) 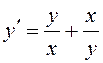 – не является линейным;
– не является линейным;
в) ![]() . Разделив обе части этого дифференциального
уравнения на
. Разделив обе части этого дифференциального
уравнения на ![]() , получим
, получим ![]()
![]() – линейное дифференциальное уравнение;
– линейное дифференциальное уравнение;
г) ![]() – не является линейным.
– не является линейным.
Одним из методов решения уравнений вида
(10.6) является метод подстановки. Идея метода состоит в том, что любая
функция может быть представлена в виде произведения двух функций, одна из
которых произвольная. Например, 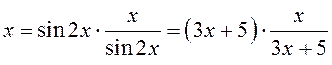 и т.д.
и т.д.
Будем искать решение дифференциального уравнения
(10.6) в виде произведения двух функций: ![]() .
Найдем
.
Найдем ![]() и подставим в уравнение:
и подставим в уравнение:
![]() .
.
Так как первый сомножитель в произведении ![]() можно выбрать произвольно, потребуем,
чтобы функция
можно выбрать произвольно, потребуем,
чтобы функция ![]() обращала в ноль первое слагаемое
в последнем равенстве:
обращала в ноль первое слагаемое
в последнем равенстве: ![]() . Тогда для нахождения
функций
. Тогда для нахождения
функций ![]() и
и ![]() получим
систему дифференциальных уравнений:
получим
систему дифференциальных уравнений:
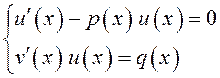 . (10.7)
. (10.7)
Так
как функция ![]() выбирается в известном смысле произвольно,
то она является каким-либо частным решением первого уравнения системы
(10.7). Заметим, что оно является линейным однородным дифференциальным уравнением
с разделяющимися переменными.
выбирается в известном смысле произвольно,
то она является каким-либо частным решением первого уравнения системы
(10.7). Заметим, что оно является линейным однородным дифференциальным уравнением
с разделяющимися переменными.
Решив первое уравнение, подставим найденную функцию ![]() во второе дифференциальное уравнение и
найдем
во второе дифференциальное уравнение и
найдем ![]() , как общее решение этого уравнения.
, как общее решение этого уравнения.
ПРИМЕР.
Решить задачу Коши 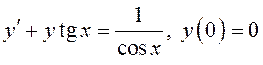 .
.
Пусть 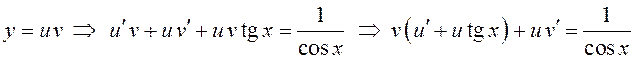 .
.
Отсюда
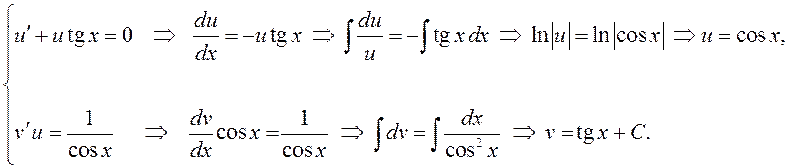
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.