Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 19

Составим и решим характеристическое уравнение:

.

Отсюда  – ф.с.р.. Зададим следующее начальное условие:  – соответствующее частное решение. При достаточно малом значении   , то есть траектория, начинаясь вблизи начала координат, с ростом  неограниченно от него удаляется. По определению это означает, что тривиальное решение  устойчивым не является, значит, неустойчивы и все частные решения данного дифференциального уравнения, а также неоднородного уравнения .

Из рассмотренных примеров можно заключить, что для линейных уравнений и систем дифференциальных уравнений с постоянными коэффициентами устойчивость или неустойчивость их решений зависит от вида корней соответствующих  характеристических уравнений. Исследуем этот вопрос подробно.

12.2.Условия устойчивости для систем линейных

однородных дифференциальных уравнений

с постоянными коэффициентами

Рассмотрим систему линейных однородных дифференциальных уравнений с постоянными коэффициентами второго порядка:

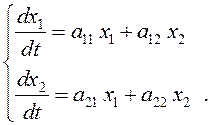                                             (12.5)

Характеристическое уравнение этой системы

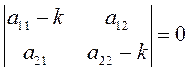                                              (12.6)

является квадратным уравнением и имеет два корня, которые могут быть действительными – различными или совпадающими – комплексными.

Рассмотрим всевозможные случаи.

1.

Так как собственные значения различны, то им соответствуют два различных собственных вектора 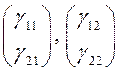  и общее решение имеет вид:

.

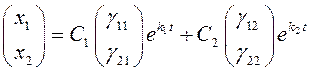Исследуем на устойчивость тривиальное решение, то есть точку покоя, расположенную в начале координат.

Пусть 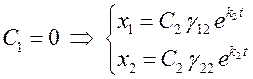. Эти равенства могут трактоваться как  параметрические уравнения соответствующей траектории. Разделив первое из них на второе, получим 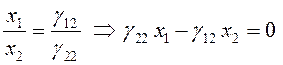 , то есть данная траектория является прямой линией.

Аналогично, полагая , получим: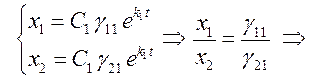

. Значит, и эта траектория – прямая. Заметим, что в обоих случаях  .

Рассмотрим теперь всевозможные варианты, когда .

Будем считать, что . Тогда 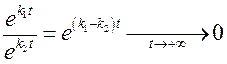, следовательно,

.

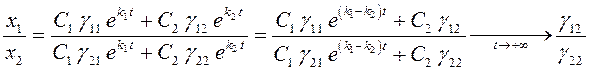Это означает, что все траектории, кроме той, что определяется значением , имеют общую касательную  и с ростом  неограниченно приближаются к началу координат, так как и в этом случае  (рис. 10).

Таким образом, точка покоя такого типа асимптотически устойчива в целом. Она называется устойчивым узлом.

2.

Анализ траекторий в этом случае аналогичен предыдущему. Точка покоя неустойчива. Она называется неустойчивым узлом (рис. 11).

3.

Так как общее решение системы  в этом случае имеет вид 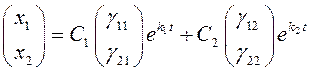,  то при  точки на  всех траекториях (кроме той, которая соответствует ) удаляются от точки покоя .

Если , то аналогично п.1 имеем 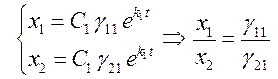, то есть траекторией является прямая линия, вдоль которой точки приближаются к началу координат.

Если , то   – прямая, вдоль которой точки удаляются от точки покоя (рис. 12). Точка покоя такого типа неустойчива, она называется седлом.

4.  – корни характеристического уравнения (12.6) чисто мнимые.

Общее решение системы в этом случае имеет вид (см.гл.11):

,

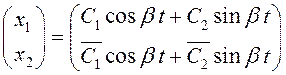где  – некоторые линейные комбинации произвольных постоянных ,.

Так как  задаются периодическими функциями, то траектории – замкнутые линии (рис. 13). Можно показать, что это эллипсы с центром в начале координат. В этом случае точка покоя устойчива, но не асимптотически. Она называется центром.

5. .

Решение в этом случае имеет вид:

.

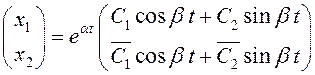Если  изменится на величину периода , то точка на траектории вернется не в прежнее положение, а станет ближе к точке покоя, так как  и , то есть движение будет происходить по спиралям (рис.14). Такая точка покоя асимптотически устойчива в целом и называется устойчивым фокусом.

6. .