Геометрический смысл задачи Коши для дифференциального уравнения первого порядка: найти интегральную кривую данного дифференциального уравнения, проходящую через заданную точку плоскости.
ОПРЕДЕЛЕНИЕ. Точки, в которых не выполняется условие теоремы Коши, называются особыми точками дифференциального уравнения.
По теореме Коши через всякую неособую точку проходит единственная интегральная кривая. Если точка является особой для данного дифференциального уравнения, то через нее либо проходит более одной интегральной кривой, либо не проходит ни одна.
ОПРЕДЕЛЕНИЕ.
Общим решением дифференциального уравнения первого порядка называется
функция ![]() , удовлетворяющая условиям:
, удовлетворяющая условиям:
1)
при любых значениях постоянной ![]() из некоторого множества
из некоторого множества ![]() является решением дифференциального уравнения;
является решением дифференциального уравнения;
2)
при любом начальном условии,
удовлетворяющем условиям теоремы Коши, найдется единственное значение ![]() такое, что
такое, что ![]() –
решение, удовлетворяющее этому условию.
–
решение, удовлетворяющее этому условию.
Решения дифференциального уравнения, полученные из
общего при конкретных значениях постоянной ![]() ,
называются частными решениями. Задача Коши является задачей отыскания
частного решения дифференциального уравнения.
,
называются частными решениями. Задача Коши является задачей отыскания
частного решения дифференциального уравнения.
Все дифференциальные уравнения первого порядка разделяются на типы, которые различаются методами, применяемыми для их решения. Рассмотрим некоторые из них.
10.2.1. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
![]() (10.4)
(10.4)
или ![]() .
.
ПРИМЕРЫ. а) 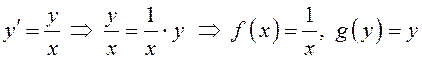 – данное уравнение
является уравнением с разделяющимися переменными;
– данное уравнение
является уравнением с разделяющимися переменными;
б) 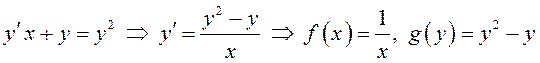 – это дифференциальное
уравнение тоже является уравнением с разделяющимися переменными;
– это дифференциальное
уравнение тоже является уравнением с разделяющимися переменными;
в) 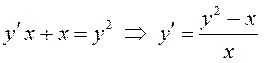 – данное уравнение не
может быть представлено в виде (10.4), поэтому не является дифференциальным
уравнением с разделяющимися переменными;
– данное уравнение не
может быть представлено в виде (10.4), поэтому не является дифференциальным
уравнением с разделяющимися переменными;
г) ![]() – дифференциальное
уравнение с разделяющимися переменными;
– дифференциальное
уравнение с разделяющимися переменными;
д) дифференциальное уравнение (10.1) является уравнением с разделяющимися переменными.
Для того чтобы решить уравнение вида (10.4), надо сначала разделить переменные, то есть преобразовать его к виду, когда в левой части равенства будет одна переменная, а в правой – другая.
Приведем алгоритм решения уравнений вида ![]() .
.
1 шаг: заменим в (10.4) ![]() на
на ![]() и перепишем уравнение:
и перепишем уравнение: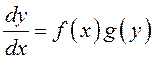 ;
;
2 шаг: умножим обе части на ![]() :
:
![]() ;
;
3 шаг: разделим обе части уравнения на ![]() , считая, что
, считая, что ![]() :
: 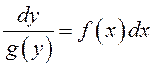 . Дифференциальное уравнение такого вида
называется уравнением с разделенными переменными;
. Дифференциальное уравнение такого вида
называется уравнением с разделенными переменными;
4 шаг: проинтегрируем обе части этого уравнения: 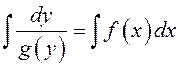 . Вычислив интеграл слева и справа, получим
общее решение дифференциального уравнения в неявном, как правило, виде, то есть
его общий интеграл.
. Вычислив интеграл слева и справа, получим
общее решение дифференциального уравнения в неявном, как правило, виде, то есть
его общий интеграл.
ЗАМЕЧАНИЕ.
При делении обеих частей уравнения на ![]() (шаг 3)
могут быть потеряны некоторые решения дифференциального уравнения: если
(шаг 3)
могут быть потеряны некоторые решения дифференциального уравнения: если ![]() , то постоянная функция
, то постоянная функция ![]() – решение, в чем легко убедиться,
подставив ее в уравнение.
– решение, в чем легко убедиться,
подставив ее в уравнение.
ПРИМЕР. Найти общее решение дифференциального уравнения
![]() .
.
Как было отмечено выше, это уравнение является дифференциальным уравнением с разделяющимися переменными
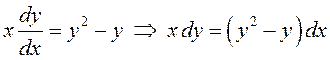 .
.
Полагая, что ![]() , получим
, получим
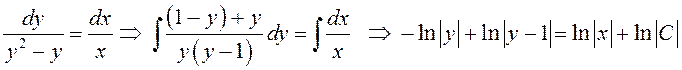 .
.
Отметим, что здесь постоянная
интегрирования для удобства дальнейших преобразований записана как ![]() . Используя свойства логарифмов, имеем:
. Используя свойства логарифмов, имеем: 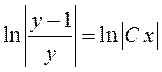 , или
, или 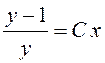 –
общий интеграл данного дифференциального уравнения (решение, записанное в неявном
виде).
–
общий интеграл данного дифференциального уравнения (решение, записанное в неявном
виде).
Заметим, что при делении на ![]() были потеряны решения
были потеряны решения ![]() и
и ![]() . Однако
решение
. Однако
решение ![]() в общем интеграле содержится (при
в общем интеграле содержится (при ![]() ), а
), а ![]() – нет. Поэтому, выразив у из
равенства
– нет. Поэтому, выразив у из
равенства 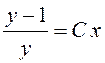 , запишем общее решение данного дифференциального
уравнения, которое состоит из функций
, запишем общее решение данного дифференциального
уравнения, которое состоит из функций ![]() .
.
ПРИМЕР. Вернемся к уравнению (10.1) и ответим на вопрос, заданный в примере на стр. 4.
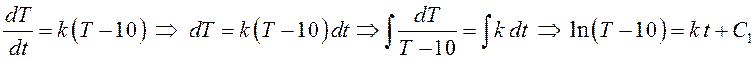 .
.
Так как по
условию задачи ![]() , то
, то ![]() . Чтобы
найти коэффициент
. Чтобы
найти коэффициент ![]() , воспользуемся вторым условием:
при
, воспользуемся вторым условием:
при ![]() температура
температура ![]() . Тогда
получим
. Тогда
получим ![]() , следовательно,
, следовательно,
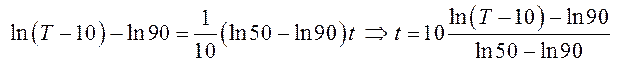 .
.
Поэтому
тело остынет до температуры ![]() за время
за время
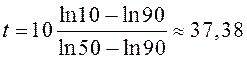 (мин.).
(мин.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.