Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 10

(10.19) и (10.20) – два уравнения для определения двух неизвестных функций .

Таким образом, если  удовлетворяют  системе двух дифференциальных уравнений

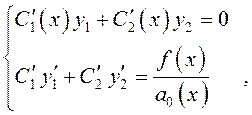                                                                    (10.21)

то  – частное решение линейного неоднородного дифференциального уравнения (10.11).

Основной  определитель  системы (10.21) 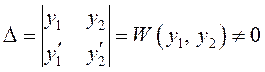    по  теореме 2, так как решения  линейно независимы. Следовательно, система (10.21) имеет единственное решение . Проинтегрировав найденные функции, найдем  и запишем частное решение.

ЗАМЕЧАНИЕ. Для неоднородного дифференциального уравнения -го порядка , , частное решение находится в виде , где   – ф.с.р. соответствующего линейного однородного дифференциального уравнения

.

Неизвестные функции  являются решением системы дифференциальных уравнений

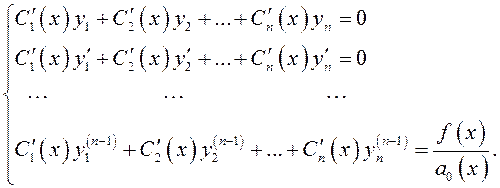
Рассмотренный метод отыскания частного решения называется методом вариации произвольных постоянных.

ПРИМЕР. Найти общее решение линейного неоднородного дифференциального уравнения .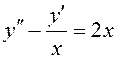

Составим и решим соответствующее однородное дифференциальное уравнение .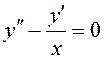 

Это уравнение допускает понижение порядка, поэтому сделаем подстановку:

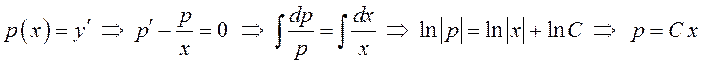
или 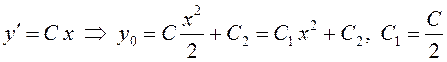  – общее решение однородного уравнения. В соответствии с теоремой 3 функции   образуют ф.с.р. этого уравнения.

Будем искать частное решение исходного неоднородного дифференциального уравнения в виде . Для того, чтобы найти неизвестные функции , составим  и решим систему (10.21):

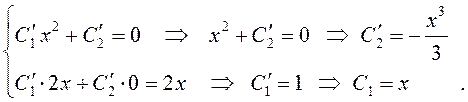
Заметим, что, так как в данном случае находится частное решение исходного неоднородного дифференциального уравнения, то достаточно найти некоторые частные решения для каждого из двух уравнений системы (10.21).

Итак, 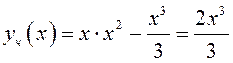, а 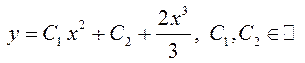 – искомое общее решение.

ПРИМЕР. Найти общее решение дифференциального уравнения

.

Решим соответствующее однородное дифференциальное уравнение    

.

Характеристическое уравнение  имеет комплексные корни  – ф.с.р., а   .

Будем искать частное решение в виде .

Составим систему уравнений (10.21):

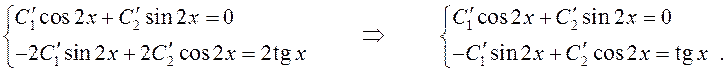
Решим последнюю систему методом Крамера (см.гл.1):

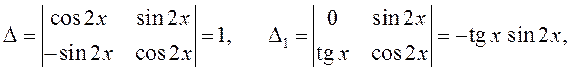
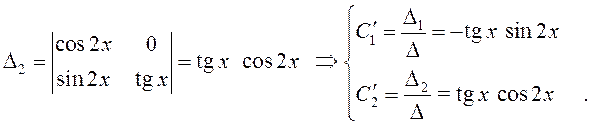
Отсюда

,

.

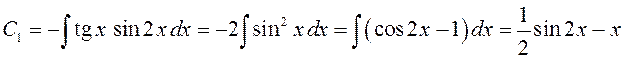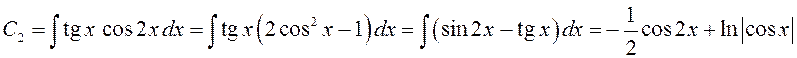Таким образом,

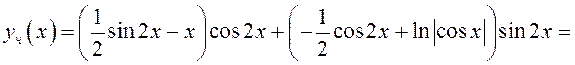
, а общим решением данного дифференциального уравнения является функция , .

10.4.2.МЕТОД  ПОДБОРА  ЧАСТНОГО  РЕШЕНИЯ

 (МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ)

Этот  метод применим только к линейным уравнениям с постоянными коэффициентами

и только в том случае, когда правая часть имеет следующий специальный вид:

   – многочлен   -ой степени,  

или

 – многочлены  -ой и  -ой степеней соответственно.

Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и правой частью специального вида I типа:

                                                    (10.22)

где .

Будем полагать, что некоторое частное решение дифференциального уравнения (10.22) имеет вид, аналогичный правой части, то есть представляется произведением  и многочлена  -ой  степени . Неизвестные коэффициенты  многочлена  подберем так, чтобы функция  

                                                 (10.23) 

обращала дифференциальное уравнение (10.22) в тождество. Для этого найдем производные

и подставим  в (10.22):

.

Сократив на  и перегруппировав слагаемые, получим:

.                      (10.24)

Заметим, что так как  – многочлен -ой степени, то  имеет степень , а   – степень .

Рассмотрим следующие случаи:

а)  не является корнем характеристического уравнения (10.15), то есть . Тогда в правой части (10.24) стоит многочлен -ой степени и в левой – также многочлен -ой степени, но с неопределенными коэффициентами. Приравнивая коэффициенты при одинаковых степенях  справа и слева, получим систему линейных алгебраических уравнений для нахождения неизвестных  .

б)  – простой корень характеристического уравнения (10.15), то есть . Тогда (10.24) не может быть тождеством: в левой части стоит многочлен степени . Поэтому в данном случае частное решение надо искать в виде произведения  и многочлена -ой степени без свободного члена, который при вычислении производной  пропадает: