Заметим, что функция ![]() не
является решением дифференциального уравнения
не
является решением дифференциального уравнения 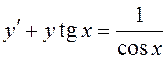 , поэтому
при разделении переменных в первом из уравнений системы обоснованно полагалось,
что
, поэтому
при разделении переменных в первом из уравнений системы обоснованно полагалось,
что ![]() .
.
Таким образом, общее решение данного дифференциального уравнения имеет вид
![]() .
.
Найдем теперь решение задачи Коши:
![]() – искомое частное
решение.
– искомое частное
решение.
10.2.4. УРАВНЕНИЯ БЕРНУЛЛИ
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение первого порядка называется уравнением Бернулли, если может быть приведено к виду
![]() ,
(10.8)
,
(10.8)
При ![]() уравнение (10.8)
является линейным, а при
уравнение (10.8)
является линейным, а при ![]() – уравнением с разделяющимися
переменными.
– уравнением с разделяющимися
переменными.
ПРИМЕРЫ. а) 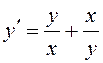 – уравнение Бернулли (
– уравнение Бернулли (![]() ). Это уравнение, кроме того, является
однородным дифференциальным уравнением первого порядка;
). Это уравнение, кроме того, является
однородным дифференциальным уравнением первого порядка;
б) 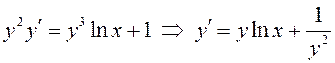 – уравнение Бернулли (
– уравнение Бернулли (![]() );
);
в) ![]() – уравнение Бернулли (
– уравнение Бернулли (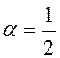 ).
).
Уравнения вида (10.8) могут быть решены так же, как и
линейные, методом подстановки: будем искать решение в виде ![]() . Подставим эту функцию в уравнение:
. Подставим эту функцию в уравнение: ![]() . Тогда функции
. Тогда функции ![]() найдутся
как решение системы дифференциальных уравнений
найдутся
как решение системы дифференциальных уравнений
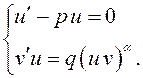
Сначала
решим первое уравнение этой системы, причем ![]() – его частное
решение. Подставив
– его частное
решение. Подставив ![]() во второе уравнение, найдем
во второе уравнение, найдем ![]() как общее решение этого дифференциального
уравнения.
как общее решение этого дифференциального
уравнения.
ПРИМЕР. Найти общее решение дифференциального уравнения ![]() .
.
Пусть ![]() .
.
Отсюда
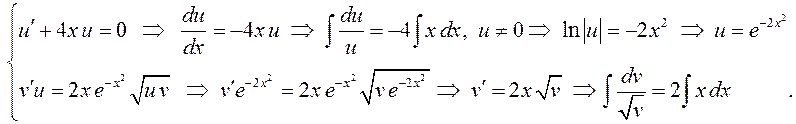
Интегрируя,
получаем ![]() , или
, или 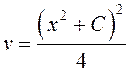 . Заметим,
что при разделении переменных в первом из этих уравнений было потеряно решение
. Заметим,
что при разделении переменных в первом из этих уравнений было потеряно решение ![]() , а, значит, и решение
, а, значит, и решение ![]() исходного дифференциального уравнения.
исходного дифференциального уравнения.
Следовательно,
общее решение имеет вид 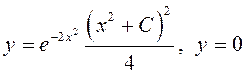 .
.
Отметим, что решение ![]() не
содержится в решении
не
содержится в решении 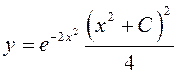 ни при каком значении постоянной
ни при каком значении постоянной
![]() .
.
10.2.5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение первого порядка вида
![]()
называется
уравнением в полных дифференциалах, если левая часть его является полным
дифференциалом некоторой функции ![]() . Это имеет место, если
. Это имеет место, если 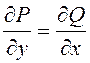 .
.
ПРИМЕРЫ. а) ![]() – это уравнение является однородным дифференциальным
уравнением первого порядка. Перепишем его таким образом:
– это уравнение является однородным дифференциальным
уравнением первого порядка. Перепишем его таким образом:
![]() . Тогда
. Тогда
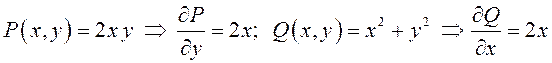 .
.
Значит, это не только однородное дифференциальное уравнение, но и уравнение в полных дифференциалах.
б) ![]() . Так
как для этого дифференциального уравнения
. Так
как для этого дифференциального уравнения 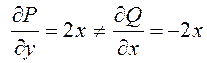 , оно
не является уравнением в полных дифференциалах, хотя, так же как и предыдущее,
является однородным дифференциальным уравнением первого порядка.
, оно
не является уравнением в полных дифференциалах, хотя, так же как и предыдущее,
является однородным дифференциальным уравнением первого порядка.
По теореме о независимости криволинейного интеграла от
пути интегрирования (см.гл. 9) для того, чтобы выражение ![]() было полным дифференциалом некоторой
функции
было полным дифференциалом некоторой
функции ![]() , необходимо и достаточно выполнение
равенства
, необходимо и достаточно выполнение
равенства 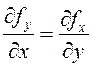 . Поэтому, если
. Поэтому, если 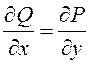 , то
существует функция
, то
существует функция ![]() такая, что ее полный дифференциал
такая, что ее полный дифференциал
![]() . Но нулевым является полный дифференциал
лишь постоянной функции, значит, если
. Но нулевым является полный дифференциал
лишь постоянной функции, значит, если ![]() –
решение уравнения
–
решение уравнения ![]() , то
, то ![]() .
.
Таким образом, для того чтобы решить дифференциальное
уравнение в полных дифференциалах, надо найти функцию ![]() ,
после чего общий интеграл уравнения запишется в виде
,
после чего общий интеграл уравнения запишется в виде ![]() .
.
ПРИМЕР.
Решить задачу Коши 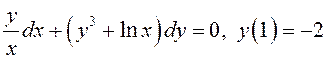 .
.
В данном уравнении 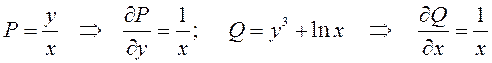 ,
поэтому данное дифференциальное уравнение является уравнением в
полных дифференциалах. Так как условие
,
поэтому данное дифференциальное уравнение является уравнением в
полных дифференциалах. Так как условие 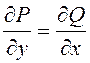 выполнено,
то существует функция
выполнено,
то существует функция ![]() такая, что
такая, что 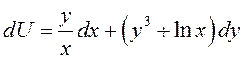 .
.
По определению полного дифференциала 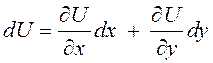 .
.
Сравнив эти два выражения, получим систему дифференциальных
уравнений для нахождения неизвестной функции ![]() :
: 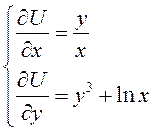 .
.
Рассмотрим
первое уравнение системы 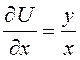 . Частная производная по
. Частная производная по
![]() , как известно (см.гл.6), вычисляется при
условии
, как известно (см.гл.6), вычисляется при
условии ![]() , поэтому чтобы найти из этого равенства
, поэтому чтобы найти из этого равенства ![]() , проинтегрируем его в том же предположении:
, проинтегрируем его в том же предположении:
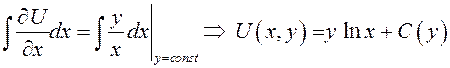 .
.
Подчеркнем,
что в рамках условия ![]() постоянная интегрирования будет
зависеть от у.
постоянная интегрирования будет
зависеть от у.
Подставим теперь найденную функцию во второе уравнение
системы: 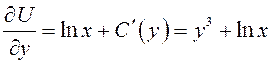 . Отсюда получим
. Отсюда получим ![]() –
уравнение для определения неизвестной функции
–
уравнение для определения неизвестной функции ![]() .
.
Найдем
ее: 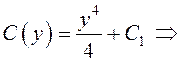
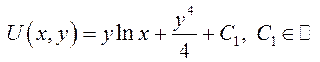 .
.
Таким
образом, общий интеграл исходного дифференциального уравнения имеет вид 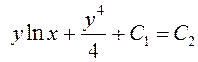 , или
, или 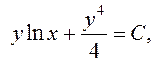 где
где ![]() .
.
По начальному условию ![]() ,
поэтому
,
поэтому 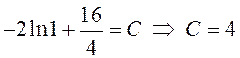 и
и
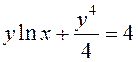 – решение поставленной задачи Коши.
– решение поставленной задачи Коши.
10.3. Дифференциальные уравнения старших порядков
Уравнение вида ![]() называется
дифференциальным уравнением
называется
дифференциальным уравнением ![]() -го порядка. Если возможно
выразить из этого равенства
-го порядка. Если возможно
выразить из этого равенства ![]() , то получим дифференциальное
уравнение
, то получим дифференциальное
уравнение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.