Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 20

Движение будет происходить также по спиралям, но в обратную сторону (рис.15). Точка покоя в этом случае называется неустойчивым фокусом.

7.

В этом случае решение системы имеет вид (см.гл.11):

.

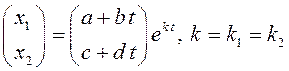Для системы второго порядка , поэтому

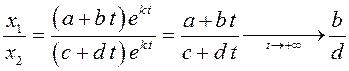, а 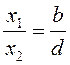 – прямая линия, значит, что все траектории имеют касательную .

Если ,  то  и касательная  сама является траекторией (рис. 16). Заметим, что так как , то с ростом  точки всех траекторий стремятся к началу координат.  Точка покоя такого типа называется вырожденным устойчивым узлом.

8.

В этом случае точка покоя является неустойчивым вырожденным узлом (рис.17).

9. .

Общее решение системы имеет вид:  .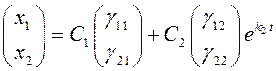

Если  то 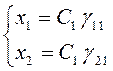 – точки покоя, расположенные на прямой .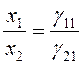

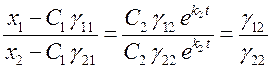Если  то , или ,

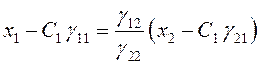то есть траекториями являются  прямые линии, параллельные прямым  (рис. 18). С ростом  точки на этих траекториях приближаются к точкам на прямой , потому что .     В этом случае точка покоя устойчива, но не асимптотически.

10. .

Точка покоя такого типа неустойчива вследствие того, что .

11. .

Общее решение имеет вид 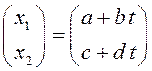 и точка покоя неустойчива.

Вывод. Для системы линейных однородных дифференциальных уравнений с постоянными коэффициентами справедливо следующее:

1.  если у всех корней характеристического уравнения (12.6) , то тривиальное решение системы асимптотически устойчиво в  целом, откуда следует, что все частные решение также асимптотически устойчивы в целом;

2.  если хотя бы один корень имеет , то тривиальное решение неустойчиво;

3.  если среди корней есть простые корни с , а остальные корни имеют , то тривиальное решение устойчиво, но не асимптотически;

4.  если среди корней есть кратные корни с , то решение практически всегда неустойчиво;

5.  вышесказанное справедливо не только для систем дифференциальных уравнений, но и для линейных дифференциальных уравнений с постоянными коэффициентами -го порядка.

12.3. Признаки отрицательности действительных частей

корней многочлена

Рассмотрим многочлен -ой степени с действительными коэффициентами

        ,                              (12.7)

.

ТЕОРЕМА (необходимое условие отрицательности действительных частей корней многочлена). Для того чтобы действительные части всех корней многочлена с действительными коэффициентами были отрицательны, необходимо, чтобы все коэффициенты многочлена были одного знака.

ДОКАЗАТЕЛЬСТВО. Рассмотрим многочлен (12.7) и будем считать, что . Данный многочлен имеет ровно  корней, действительных или комплексных, а так как все его коэффициенты действительны, то комплексные корни встречаются комплексно сопряженными парами, то есть корни (12.7) имеют вид:   или  .

При разложении (12.7) на множители корню  соответствует множитель вида , коэффициенты которого положительны.

Паре комплексно сопряженных корней соответствуют два множителя

. Так как по условию , то и здесь все коэффициенты положительны.

Таким образом, при разложении  на множители получим произведение линейных и квадратичных сомножителей с положительными коэффициентами. Следовательно, после раскрытия скобок все коэффициенты многочлена будут положительными.  Кроме  того,  так  как   , многочлен  будет содержать все степени    от  -ой  до  нулевой, то есть среди его коэффициентов нулевых тоже не будет. Что и требовалось доказать.

ЗАМЕЧАНИЕ. Сформулированное необходимое условие не является достаточным для всех многочленов старше второй степени. Для квадратного трехчлена положительность всех его коэффициентов – необходимое и достаточное условие того, что . Это очевидным образом следует из теоремы Виета.