Заметим, что
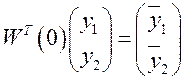 , где
, где 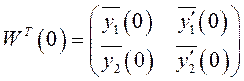 – транспонированная
матрица Вронского для решений
– транспонированная
матрица Вронского для решений ![]() , вычисленная в точке
, вычисленная в точке ![]() . Поэтому нормальная система
фундаментальных функций с единичной матрицей в нуле может быть найдена из
произвольной таким образом:
. Поэтому нормальная система
фундаментальных функций с единичной матрицей в нуле может быть найдена из
произвольной таким образом:
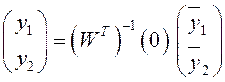 .
.
Если общее решение однородного дифференциального уравнения (10.30) составить из фундаментальных функций с единичной матрицей в нуле, именно
![]() ,
(10.32)
,
(10.32)
![]() , то вследствие (10.31) такая форма
представления решения будет обладать замечательным свойством:
, то вследствие (10.31) такая форма
представления решения будет обладать замечательным свойством:![]() . Это означает, что произвольные
постоянные равны значению функции
. Это означает, что произвольные
постоянные равны значению функции ![]() и ее производной в
точке
и ее производной в
точке ![]() .
.
Особо подчеркнем свойства последней фундаментальной
функции ![]() : она является решением однородного дифференциального
уравнения (10.30) и, кроме того,
: она является решением однородного дифференциального
уравнения (10.30) и, кроме того, ![]() .
.
Частное решение неоднородного уравнения (10.29) может быть представлено в виде
 .
(10.33)
.
(10.33)
Покажем это, для чего подставим (10.33) в уравнение (10.29).
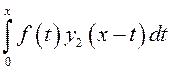 представляет собой интеграл с переменным
верхним пределом, зависящий от параметра
представляет собой интеграл с переменным
верхним пределом, зависящий от параметра ![]() .
Выведем формулу вычисления производной такого интеграла.
.
Выведем формулу вычисления производной такого интеграла.
Рассмотрим
функцию  . По определению производной
. По определению производной
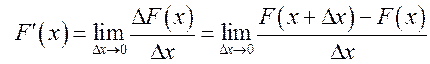 .
.
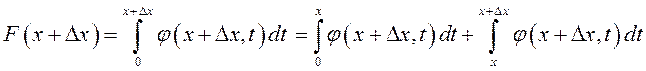 вследствие
свойства аддитивности определенного интеграла. Полагая функцию
вследствие
свойства аддитивности определенного интеграла. Полагая функцию ![]() непрерывной, применим к последнему
интегралу теорему о среднем значении (см. п.8.2):
непрерывной, применим к последнему
интегралу теорему о среднем значении (см. п.8.2):
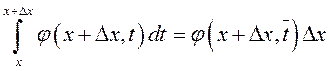 , где
, где ![]() находится между
находится между ![]() и
и
![]() .
.
Тогда
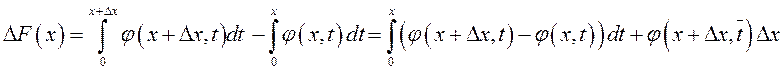 .
.
Отсюда имеем:
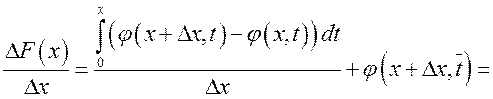
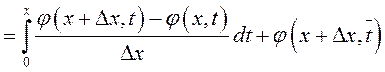 , так
как
, так
как ![]() не зависит от
не зависит от ![]() .
Переходя к пределу при
.
Переходя к пределу при ![]() , получим, что
, получим, что
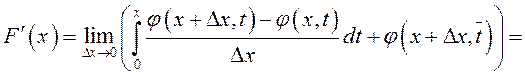
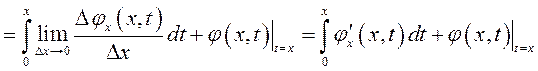 . (10.34)
. (10.34)
Пользуясь формулой (10.34), найдем производные частного решения (10.33):

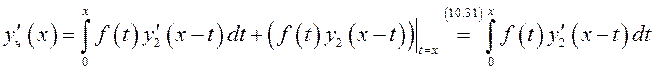 ,
,
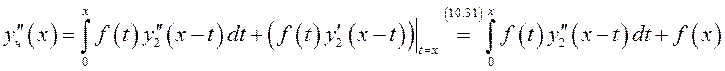 .
.
Заметим, что
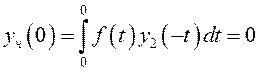 , а также
, а также 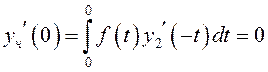 .
.
Подставим
![]() и найденные производные в (10.29):
и найденные производные в (10.29):
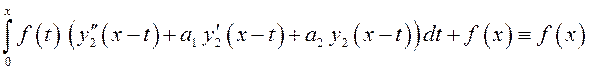 , так
как
, так
как ![]() – решение однородного дифференциального
уравнения (10.30).
– решение однородного дифференциального
уравнения (10.30).
Итак, (10.33) – действительно, одно из частных решений уравнения (10.29), а потому общее решение этого дифференциального уравнения получаем в виде:
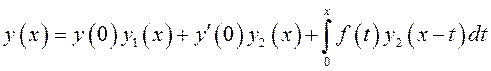 . (10.35)
. (10.35)
Представление решения дифференциального уравнения (10.29) в виде (10.35) удобно по двум причинам:
1) произвольные постоянные имеют вполне определенный смысл, а потому решение задачи Коши можно найти сразу, не находя общего решения уравнения;
2) частное решение в виде (10.33) может быть найдено не только для непрерывной, но и для кусочно-непрерывной правой части.
Такой метод решения задачи Коши для дифференциального уравнения (10.29) называется методом Коши, а решение (10.35) – решением в форме Коши.
ПРИМЕР.
Решить задачу Коши: ![]() .
.
1. Решим соответствующее данному однородное дифференциальное уравнение ![]() . Его характеристическое уравнение имеет
вид:
. Его характеристическое уравнение имеет
вид:
![]()
![]() .
.
2. Проверим, является ли найденная ф.с.р. нормальной системой фундаментальных функций с единичной матрицей в нуле (см.(10.31):
![]() – значит, решение
– значит, решение ![]() не
подходит;
не
подходит;
![]() – значит, решение
– значит, решение ![]() подходит.
подходит.
Заметим,
что так как по условию ![]() , в решении (10.35) функция
, в решении (10.35) функция ![]() не будет использоваться, а потому мы ее и
не будем искать.
не будет использоваться, а потому мы ее и
не будем искать.
3. Выпишем решение задачи Коши (10.35) при ![]()
![]() :
:
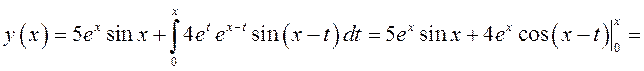
![]() .
.
ПРИМЕР.
Решить задачу Коши: ![]() , где
, где 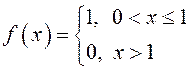 (рис.
3).
(рис.
3).
|
1.
Решим соответствующее данному однородное дифференциальное уравнение 2. Проверим, является ли найденная ф.с.р. нормальной системой фундаментальных функций с единичной матрицей в нуле:
|
3. Найдем нормальную систему фундаментальных функций с
единичной матрицей в нуле ![]() . Очевидно,
. Очевидно, ![]() , а
, а ![]() будем
искать в виде
будем
искать в виде ![]() . Для определения неизвестных постоянных
. Для определения неизвестных постоянных
![]() получаем систему линейных уравнений:
получаем систему линейных уравнений:
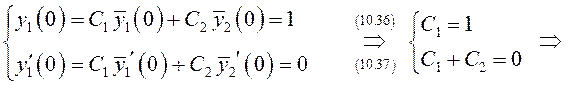
![]() .
.
Таким
образом, ![]() .
.
4. Выпишем решение задачи Коши (10.35):
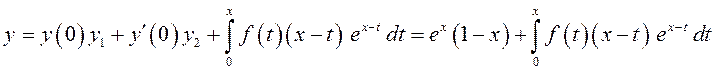 .
.
Вычислим интеграл:
если ![]() ,
то (см. рис.3)
,
то (см. рис.3)
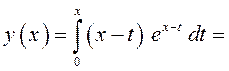
![]() ;
;
если ![]() , то
, то
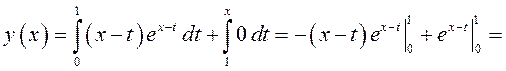
![]() .
.
Таким образом, решение поставленной задачи Коши имеет вид:
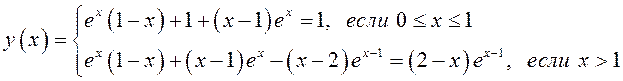 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.