![]() , (10.9)
, (10.9)
которое называется уравнением, разрешенным относительно старшей производной.
График какого-либо решения дифференциального уравнения (10.9) называется его интегральной кривой.
ТЕОРЕМА Коши
(о существовании и единственности решения дифференциального уравнения ![]() -го порядка). Пусть функция
-го порядка). Пусть функция ![]() непрерывна вместе с
непрерывна вместе с 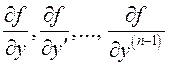 в некоторой области
в некоторой области ![]() изменения переменных
изменения переменных ![]() . Тогда для любой точки
. Тогда для любой точки ![]() существует, причем единственное решение дифференциального
уравнения (10.9), удовлетворяющее начальным условиям
существует, причем единственное решение дифференциального
уравнения (10.9), удовлетворяющее начальным условиям
![]() .
(10.10)
.
(10.10)
Без доказательства.
Задачей Коши
для дифференциального уравнения ![]() -го порядка называется
задача отыскания его решения, удовлетворяющего начальным условиям (или
условиям Коши) (10.10).
-го порядка называется
задача отыскания его решения, удовлетворяющего начальным условиям (или
условиям Коши) (10.10).
Для дифференциального уравнения второго порядка,
например, задача Коши ставится таким образом: найти решение дифференциального
уравнения ![]() , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям ![]() .
.
Геометрический смысл этой задачи состоит в следующем: требуется найти интегральную кривую
данного дифференциального уравнения, которая проходит через точку ![]() и имеет в этой точке заданную касательную
(касательную с угловым коэффициентом
и имеет в этой точке заданную касательную
(касательную с угловым коэффициентом ![]() ).
).
ОПРЕДЕЛЕНИЕ.
Общим решением дифференциального уравнения ![]() -го
порядка называется функция
-го
порядка называется функция ![]() , удовлетворяющая следующим
условиям:
, удовлетворяющая следующим
условиям:
1) при любых значениях постоянных ![]() из некоторого множества она является
решением дифференциального уравнения;
из некоторого множества она является
решением дифференциального уравнения;
2) для любых начальных условий ![]() ,
удовлетворяющих условиям теоремы Коши, существует единственный набор
постоянных
,
удовлетворяющих условиям теоремы Коши, существует единственный набор
постоянных ![]() такой, что функция
такой, что функция ![]() является
решением, удовлетворяющим этим начальным условиям.
является
решением, удовлетворяющим этим начальным условиям.
10.3.1.УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Рассмотрим некоторые типы дифференциальных уравнений старшего порядка, порядок которых можно понизить, сделав подходящую замену переменной.
1.
Дифференциальные уравнения вида ![]() .
.
Чтобы
решить уравнение такого вида, надо обе его части проинтегрировать последовательно
![]() раз.
раз.
ПРИМЕР.
Найти общее решение дифференциального уравнения 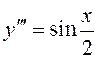 .
.
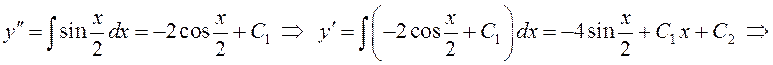
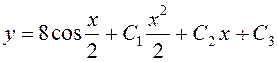 .
.
2.
Дифференциальные уравнения вида ![]() .
.
Эти уравнения второго порядка, в которых явно не
присутствует ![]() (или в общем виде
(или в общем виде ![]() .
.
Подстановка
![]() приводит данное уравнение к дифференциальному
уравнению первого порядка:
приводит данное уравнение к дифференциальному
уравнению первого порядка: 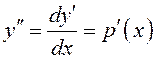
![]() .
Решив это уравнение, найдем функцию
.
Решив это уравнение, найдем функцию ![]() , а затем
, а затем ![]() .
.
ПРИМЕР. Найти решение дифференциального уравнения (10.2)
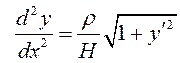 , которое
удовлетворяет начальным условиям
, которое
удовлетворяет начальным условиям ![]() (см. пример на стр. 4 из
п. 10.1).
(см. пример на стр. 4 из
п. 10.1).
Обозначим
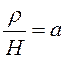 . Уравнение
. Уравнение 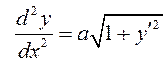 не
содержит явно
не
содержит явно ![]() , поэтому сделаем подстановку
, поэтому сделаем подстановку ![]() , после которой получим дифференциальное
уравнение первого порядка с разделяющимися переменными:
, после которой получим дифференциальное
уравнение первого порядка с разделяющимися переменными:
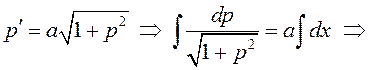
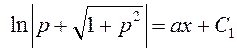 .
.
Из начального условия ![]() следует, что
следует, что ![]() . Отсюда
. Отсюда
![]() .
.
Чтобы
выразить из этого равенства ![]() , умножим обе его части
на сопряженное выражение:
, умножим обе его части
на сопряженное выражение: 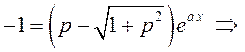
![]() .
.
Сложим 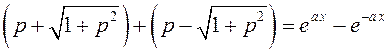 ,
откуда получим
,
откуда получим
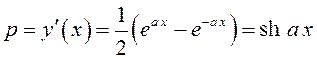 и
и 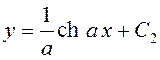 .
.
По
условию ![]()
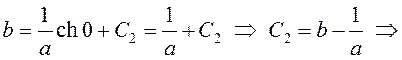
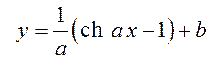 – искомое уравнение цепной
линии.
– искомое уравнение цепной
линии.
3.
Дифференциальное уравнение вида ![]() .
.
Это уравнение второго порядка, в котором явно не
присутствует ![]() . Подстановка
. Подстановка ![]() приводит
данное уравнение к дифференциальному уравнению первого порядка:
приводит
данное уравнение к дифференциальному уравнению первого порядка:
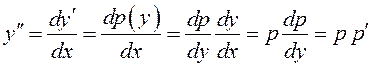 и
и ![]() –
уравнение относительно новой переменной
–
уравнение относительно новой переменной ![]() .
.
ПРИМЕР.
Решим задачу о второй космической скорости: найти с какой наименьшей скоростью ![]() надо бросить тело вертикально вверх, чтобы
оно не вернулось на Землю.
надо бросить тело вертикально вверх, чтобы
оно не вернулось на Землю.
Пусть ![]() – расстояние от центра
Земли до центра массы тела, тогда
– расстояние от центра
Земли до центра массы тела, тогда
![]() – скорость тела, а
– скорость тела, а ![]() –
ускорение. Согласно закону Ньютона
–
ускорение. Согласно закону Ньютона 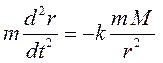 , где
, где ![]() – масса тела,
– масса тела, ![]() – масса
Земли,
– масса
Земли, ![]() гравитационная постоянная.
гравитационная постоянная.
Таким
образом, уравнение движения тела имеет вид: 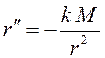 . Оно
не содержит явно время
. Оно
не содержит явно время ![]() , поэтому обозначим скорость
, поэтому обозначим скорость 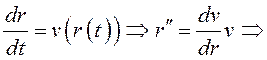
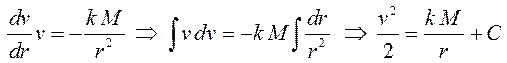 .
.
На поверхности Земли ![]() ,
поэтому
,
поэтому 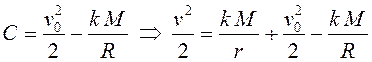 .
.
Если
тело неограниченно удаляется от поверхности Земли, то ![]() ,
при этом
,
при этом ![]() , значит
, значит
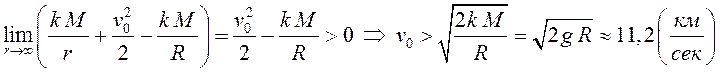 , где
, где ![]() –
радиус Земли,
–
радиус Земли, ![]() – ускорение силы тяжести на ее
поверхности.
– ускорение силы тяжести на ее
поверхности.
10.3.2. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ![]() -го ПОРЯДКА
-го ПОРЯДКА
ОПРЕДЕЛЕНИЕ.
Линейным дифференциальным уравнением ![]() -го порядка
называется уравнение вида
-го порядка
называется уравнение вида
![]() , где
, где
![]() .
.
Если ![]() , то уравнение
называется линейным неоднородным дифференциальным уравнением,
если же
, то уравнение
называется линейным неоднородным дифференциальным уравнением,
если же ![]() , то уравнение называется линейным
однородным.
, то уравнение называется линейным
однородным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.