Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 22

Замена исследования устойчивости тривиального решения системы (12.9) исследованием устойчивости тривиального решения системы (12.10) называется исследованием устойчивости решения системы (12.9) по первому приближению.

При составлении системы первого приближения можно пользоваться тем, что в окрестности нуля  (при ) следующие величины эквивалентны (см.гл.4):

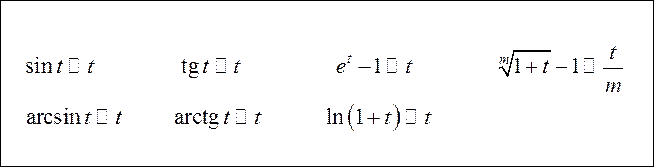.    (12.11)

ПРИМЕР. Исследовать устойчивость нулевого решения системы дифференциальных уравнений  .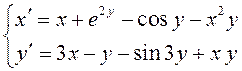

Исследуем по первому приближению устойчивость решения  этой системы

При  достаточно близких к нулю слагаемые  и  имеют более высокий порядок малости, чем  х  и  у,поэтому ими можно пренебречь при составлении системы первого приближения. Кроме того, в соответствии с (12.11) в окрестности нуля ,

.

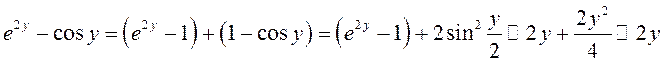Таким образом, система первого приближения имеет вид:  .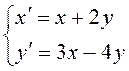

Составим ее характеристическое уравнение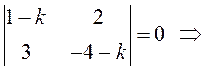   

. Один из корней этого уравнения положительный, значит, тривиальное решение обеих систем неустойчиво.

ПРИМЕР. Исследовать устойчивость нулевого решения системы дифференциальных уравнений   .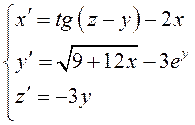

В соответствии с (12.11)

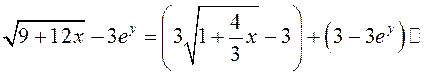
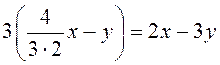, отсюда система первого приближения имеет вид:

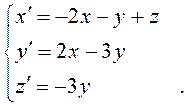
Характеристическое уравнение этой системы:

.

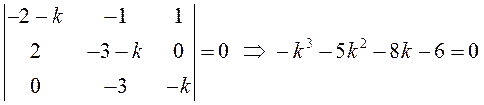Применим к многочлену  критерий Льенара-Шипара: , 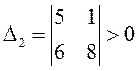. Следовательно, , поэтому  нулевое решение системы первого приближения, а также и  исходной системы асимптотически устойчиво.

Исследование устойчивости решения системы (12.9) по первому приближению возможно, если

1.  все собственные значения системы первого приближения (12.10) имеют отрицательные действительные части. В этом случае тривиальное решение системы (12.10) асимптотически устойчиво, откуда следует асимптотическая устойчивость тривиального решения исходной системы (12.9);

2.  среди собственных значений системы (12.10) есть хотя бы одно с положительной действительной частью. В этом случае тривиальное решение (12.10) неустойчиво, поэтому неустойчиво и тривиальное решение исходной системы (12.9).

Если окажется, что среди собственных значений есть такие, что , а остальные собственные значения, если они есть, имеют , то на устойчивость нулевого решения начинают влиять нелинейные слагаемые, которые отбрасываются при составлении системы первого приближения.

ПРИМЕР. Исследовать на устойчивость нулевое решение системы дифференциальных уравнений .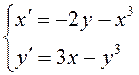

Составим систему первого приближения, отбросив нелинейные слагаемые: 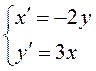. Характеристическое уравнение  имеет чисто мнимые корни  , поэтому для системы первого приближения точка покоя – центр, она устойчива, но не асимптотически. Траекториями являются замкнутые линии (эллипсы) (рис.19).

Но так как в исходной системе есть нелинейные слагаемые, то в результате их влияния траектории перестанут быть замкнутыми, однако как именно они себя поведут, исследуя систему первого приближения, узнать нельзя (рис.20).

Поэтому в таком случае метод исследования устойчивости решения по первому приближению неприменим, и надо воспользоваться более  общим, но гораздо более сложным методом функций Ляпунова.

12.5. Метод функций Ляпунова

Метод функций Ляпунова позволяет исследовать устойчивость решений систем дифференциальных уравнений с помощью специально построенных функций, так называемых функций Ляпунова, не находя самих решений системы.

Обсудим идею метода.

Рассмотрим систему дифференциальных уравнений (12.1):

   .

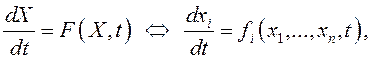
Пусть эта система имеет тривиальное решение, то есть . Как было показано ранее, все решения системы в смысле устойчивости ведут себя так же, как тривиальное решение.

Пусть  – некоторое решение (12.1), которое определяет соответствующую ему траекторию. 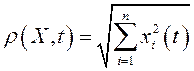 – расстояние  от  точек  на  этой траектории  до  начала  координат. Найдем  его  полную производную

по времени (см.гл.6 и рис. 21): . Заметим, что даже если сама траектория неизвестна, найденная производная – известная функция. Если , то расстояние от точек