Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 24

Пусть  – произвольная точка этой -окрестности.

Начальные условия 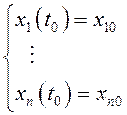   определяют  некоторое  решение  системы (12.12). Соответствующая траектория начинается в точке  (рис. 22). При движении вдоль этой траектории функция  не убывает, так как по условию 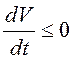 или 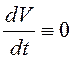, поэтому  . Это  означает,  что траектория не выйдет за пределы -окрестности, так как в противном случае она пересечет границу , на которой  . 

Таким образом, по определению точка покоя системы (12.12) устойчива.

Что и требовалось доказать.

Вернемся к ранее рассмотренному, но нерешенному примеру (см.стр. 78).

ПРИМЕР. Исследовать на устойчивость нулевое решение системы дифференциальных уравнений .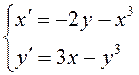

Как было показано, исследовать на устойчивость по первому приближению  нулевое решение этой системы нельзя. Поэтому воспользуемся методом функций Ляпунова.

Будем искать функцию Ляпунова в виде . Найдем ее производную в силу системы:

.

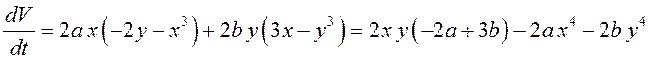Произведение  может принимать значения разных знаков, поэтому подберем параметры  и  так, чтобы . Например, . Тогда производная положительно определенной функции  в силу данной  системы  .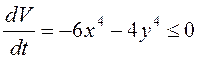

По теореме Ляпунова об устойчивости нулевое решение данной системы устойчиво.

ПРИМЕР. Исследовать на устойчивость нулевое решение системы дифференциальных уравнений .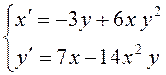

Система первого приближения имеет вид 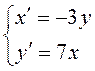. Легко убедиться, что ее  собственные значения чисто мнимые, значит, для исследования устойчивости следует воспользоваться методом функций Ляпунова.

Снова попробуем найти функцию Ляпунова в виде .

.

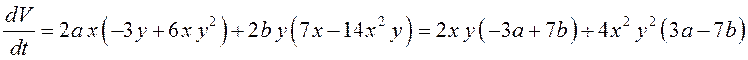При 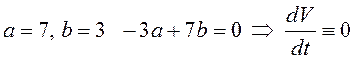, а функция  положительно определена.

Следовательно, по теореме Ляпунова об устойчивости нулевое решение данной системы устойчиво.

ТЕОРЕМА (Ляпунова об асимптотической устойчивости). Пусть в некоторой -окрестности начала координат существует дифференцируемая функция , положительно определенная в этой окрестности, производная в силу системы которой отрицательно определена. Тогда тривиальное решение системы (12.12) асимптотически устойчиво.

Без доказательства.

ПРИМЕР. Вернемся еще раз к системе 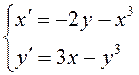. Выше для нее была найдена функция Ляпунова  и найдена производная в силу системы 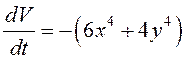, которая является отрицательно определенной функцией. Следовательно, по теореме об асимптотической устойчивости тривиальное решение этой системы асимптотически устойчиво.

ПРИМЕР. Для системы 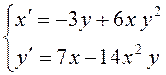 также была найдена функция Ляпунова , производная которой в силу системы 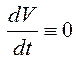. В этом случае сразу утверждать, что точка покоя устойчива, но не асимптотически  нельзя, так как сформулированная теорема дает достаточное, но не необходимое условие асимптотической устойчивости. Однако из равенства 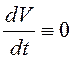 следует, что вдоль траекторий , а это означает, что все траектории – эллипсы. Поэтому точка покоя устойчива, но асимптотической устойчивости нет.

ТЕОРЕМА (Лассаля об асимптотической устойчивости в целом). Если существует функция , определенная на всем пространстве и удовлетворяющая условиям теоремы Ляпунова об асимптотической устойчивости, причем  при 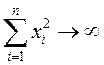, то тривиальное решение системы (12.12) асимптотически устойчиво в целом.

Без доказательства.

ПРИМЕР. Функция Ляпунова  при . Как было отмечено выше, она удовлетворяет условиям теоремы об асимптотической устойчивости, поэтому по теореме Лассаля нулевое решение системы 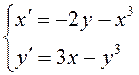  асимптотически устойчиво в целом.

ТЕОРЕМА (Четаева о неустойчивости). Пусть для системы (12.12) существует дифференцируемая функция , удовлетворяющая следующим условиям:

1)  в любой -окрестности начала координат существует область , во всех внутренних точках которой , причем  в тех граничных точках , которые являются внутренними для данной окрестности;

2)  начало координат  является граничной точкой области ;

3)  всюду в  производная в силу системы  .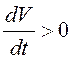

Тогда нулевое решение системы (12.12) неустойчиво.

Без доказательства.