Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений), страница 25

ПРИМЕР. Исследовать на устойчивость нулевое решение системы дифференциальных уравнений  .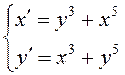  

Рассмотрим функцию . Убедимся, что она удовлетворяет условиям 1) – 3) теоремы Четаева.  

1. . Часть любой -окрестности, задаваемая этим неравенством, является областью   (рис. 23): действительно, на границе , то есть при , , а во внутренних точках   . 2. Начало координат  является граничной точкой .

3. Производная в силу данной системы

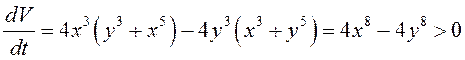, если , то есть 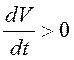   во  всех  внутренних  точках  .  Поэтому  нулевое  решение  системы неустойчиво.

ЗАМЕЧАНИЕ. Если в некоторой окрестности начала координат функция  и ее производная в силу системы  положительно определены, то все условия теоремы Четаева выполнены, следовательно, точка покоя  неустойчива.

ЗАМЕЧАНИЕ.  Метод функций  Ляпунова универсален и эффективен, но, недостаток метода в том, что не существует конструктивного  алгоритма построения функции Ляпунова для произвольной системы дифференциальных уравнений. В простейших случаях можно искать функцию Ляпунова в виде  и т.д.. Для системы дифференциальных уравнений вида

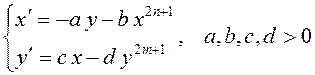
функция  является функцией Ляпунова. Точка покоя  такой системы асимптотически устойчива.

ЗАМЕЧАНИЕ. При исследовании устойчивости произвольного решения системы дифференциальных уравнений  следует сделать замену переменной , преобразовав исходную систему к системе дифференциальных уравнений, имеющей нулевое решение.

ПРИМЕР. Найти все положения равновесия системы 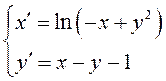    и исследовать их на устойчивость.

Чтобы найти все положения равновесия данной системы, надо найти точки, в которых правые части обоих дифференциальных уравнений одновременно обращаются в нуль:

  – положения равновесия, или точки покоя.

1)  Исследуем на устойчивость точку .

Пусть , то есть . Подставив  в систему дифференциальных уравнений, получим: .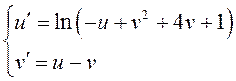

Легко убедиться, что эта система имеет тривиальное решение  Чтобы исследовать его на устойчивость, составим систему первого приближения в соответствии с (12.11): 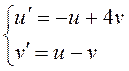. Характеристическое уравнение этой системы: 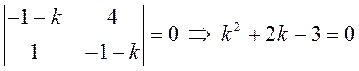. Так как , то нулевое решение неустойчиво, а, значит, точка  – неустойчивое положение равновесия.

2)  Исследуем на устойчивость точку .

Аналогично, сделав замену переменных , получим систему дифференциальных уравнений: 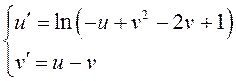, для которой система первого приближения имеет вид: 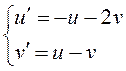. Характеристическое уравнение этой системы: 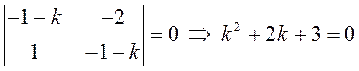. Все коэффициенты квадратного уравнения положительны, значит  и точка  – положение устойчивого равновесия.

Библиографический список

1.  Пискунов, Н.С. Дифференциальное и интегральное исчисления /     Н.С. Пискунов.– М.: Интеграл–пресс, 2005.– Т.1, 2.

2.   Араманович  И. Г .,  Лунц   Г . Л .,  Эльсгольц   Л . Э .  Функции   комплексного   переменного .  Операционное   исчисление .  Теория   устойчивости . М.: Наука, 1970.– 415 c.

3.  Краснов М. Л ., Киселев А.И., Макаренко Г.И. Функции комплексного переменного.  Операционное   исчисление . Теория  устойчивости . М.: Наука, 1981.– 304 c.

4.  Филиппов, А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: Регулярная и хаотическая динамика, 2000.–176 с.

Редактор

Компьютерная верстка, дизайн обложки

ИД № 06039 от 12.10.2001 г.

Сводный темплан 2011 г.

Подписано в печать     .  .  . Формат 60×84  ¹/₁₆. Бумага офсетная.

Отпечатано на дупликаторе. Усл. печ. л.      . Уч.-изд. л.          .

Тираж      . Заказ  .

______________________________________________________

Издательство ОмГТУ. 644050, г. Омск, пр-т Мира, 11

Типография ОмГТУ