ПРИМЕР.
Уравнение вынужденных колебаний груза, подвешенного к концу пружины, под
действием периодической возмущающей силы ![]() имеет
вид:
имеет
вид: ![]() , где
, где ![]() –
собственная частота пружины,
–
собственная частота пружины, ![]() – частота возмущающей силы.
– частота возмущающей силы.
Найти закон движения груза, если ![]() .
.
Пусть ![]() ¸
¸ ![]() ,
, ![]() , тогда
решение этой задачи сводится к решению задачи Коши
, тогда
решение этой задачи сводится к решению задачи Коши ![]() ,
, ![]() .
.
Составим и решим характеристическое уравнение: ![]() . Отсюда
. Отсюда ![]() –
общее решение соответствующего однородного дифференциального уравнения (см.
п.10.3.3).
–
общее решение соответствующего однородного дифференциального уравнения (см.
п.10.3.3).
Правая часть
![]() неоднородного дифференциального уравнения является
правой частью специального вида II типа. Сравнение этой функции с общим видом такой
правой части показывает, что
неоднородного дифференциального уравнения является
правой частью специального вида II типа. Сравнение этой функции с общим видом такой
правой части показывает, что ![]() . Комплексное число
. Комплексное число ![]() не является корнем
характеристического уравнения, поэтому в соответствии с (10.27)
не является корнем
характеристического уравнения, поэтому в соответствии с (10.27)
![]() .
.
После подстановки в исходное дифференциальное уравнение получим:
![]() .
.
Отсюда
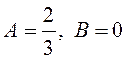 и
и 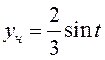 . По
теореме 4 о структуре общего решения линейного неоднородного дифференциального
уравнения общее решение имеет вид
. По
теореме 4 о структуре общего решения линейного неоднородного дифференциального
уравнения общее решение имеет вид
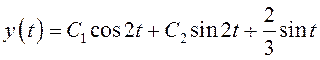 .
.
По условию ![]()
![]()
![]() ;
; 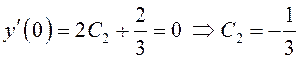 .
.
Откуда
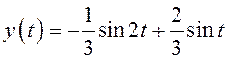 – по такому закону совершаются колебания
груза в рассматриваемом примере, когда частота возмущающей силы не совпадает
с собственной частотой пружины. В этом случае амплитуда колебаний –
наибольшее отклонение груза от положения равновесия – с течением времени не меняется
и остается ограниченной:
– по такому закону совершаются колебания
груза в рассматриваемом примере, когда частота возмущающей силы не совпадает
с собственной частотой пружины. В этом случае амплитуда колебаний –
наибольшее отклонение груза от положения равновесия – с течением времени не меняется
и остается ограниченной: ![]() .
.
Выясним, каким будет уравнение движения груза, если ![]() .
.
Для
этого решим аналогичную задачу Коши для уравнения ![]() .
.
Сравнивая
правую часть ![]() с общим видом специальной правой
части II типа, видим, что
с общим видом специальной правой
части II типа, видим, что ![]() . Комплексное число
. Комплексное число ![]() является корнем характеристического
уравнения, потому в соответствии с (10.28)
является корнем характеристического
уравнения, потому в соответствии с (10.28)
![]()
![]()
![]()
![]() .
.
После
подстановки в уравнение получим: ![]() , откуда
, откуда 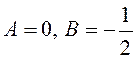 и частным решением в этом случае является
функция
и частным решением в этом случае является
функция 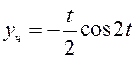 . Тогда
. Тогда 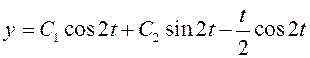 –
общее решение дифференциального уравнения
–
общее решение дифференциального уравнения ![]() .
.
По условию ![]()
![]()
![]() ;
; 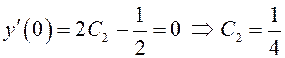 .
Следовательно
.
Следовательно 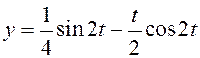 – уравнение движения груза.
Очевидно, что с течением времени амплитуда этих колебаний неограниченно
растет:
– уравнение движения груза.
Очевидно, что с течением времени амплитуда этих колебаний неограниченно
растет: ![]() . В таком случае говорят, что наступает резонанс.
. В таком случае говорят, что наступает резонанс.
Итак, резонанс наступает тогда, когда частота внешней силы совпадает с собственной частотой колебаний пружины.
10.4.3. МЕТОД КОШИ РЕШЕНИЯ ЛИНЕЙНЫХ
НЕОДНОРОДНЫХ УРАВНЕНИЙ
Метод Коши имеет два несомненных преимущества перед всеми ранее рассмотренными методами поиска частного решения линейного дифференциального уравнения. Во-первых, этим методом можно решать линейные дифференциальные уравнения с постоянными коэффициентами и любой кусочно-непрерывной правой частью, во-вторых, при решении практических задач (в механике, математической физике, сопротивлении материалов и т.д.) метод Коши позволяет, не находя общего решения, сразу найти частное решение, удовлетворяющее поставленным начальным условиям.
Рассмотрим этот метод на примере линейного дифференциального уравнения второго порядка. Оно должно быть приведенным, то есть коэффициент при старшей производной должен быть равен единице:
![]() (10.29)
(10.29)
![]()
По
теореме 4 о структуре общего решения линейного неоднородного дифференциального
уравнения общее решение уравнения (10.29) имеет вид ![]() , где
, где ![]() – общее решение соответствующего
однородного уравнения
– общее решение соответствующего
однородного уравнения
![]() ,
(10.30)
,
(10.30)
а ![]() – некоторое частное решение уравнения (10.29).
Общее решение
– некоторое частное решение уравнения (10.29).
Общее решение ![]() дифференциального уравнения
(10.30) содержит две произвольные постоянные и находится в виде
дифференциального уравнения
(10.30) содержит две произвольные постоянные и находится в виде ![]() , где решения
, где решения ![]() образуют
фундаментальную систему решений.
образуют
фундаментальную систему решений.
Так как линейная комбинация любых решений линейного
однородного дифференциального уравнения (10.30) – тоже решение (п.10.3.2,
теорема 1), то можно найти сколько угодно ф.с.р.. Из всех них выделим одну
систему фундаментальных функций ![]() , каждая из которых,
являясь решением однородного уравнения (10.30), удовлетворяет следующим условиям:
, каждая из которых,
являясь решением однородного уравнения (10.30), удовлетворяет следующим условиям:
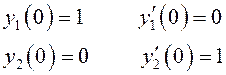 .
(10.31)
.
(10.31)
Такая система называется нормальной системой фундаментальных функций с единичной матрицей в нуле.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.