Анализ режимов работы систем автоматического управления показывает, что их нагрузочный момент представляет собой, как правило, случайные функции времени. Действительно, на примере следящей системы радиолокационной антенны (см. рис. 15.7,д и 15.8) очевидно, что, например, момент сопротивления движению определяется скоростью ветра и его направлением, а необходимые параметры движения (угловые скорость и ускорение) зависят от скорости и направления пролетающего самолета, а также его удаленности от станции. Поэтому расчет моментов сопротивления, токов и скорости, а следовательно, и мощности двигателя носит приближенный характер. Нередко запасы по мощности и времени допустимой работы таких двигателей значительно превышают средние или эквивалентные значения.
Если выбрать двигатель со значительным завышением мощности, то это приведет, с одной стороны, к увеличению габаритов и массы привода, к повышенному расходу энергии, запас которой в бортовых системах автоматики нередко ограничен, с другой стороны, отрицательно скажется на динамических свойствах системы, потому что запас мощности двигателя будет затрачиваться на «разгон самого себя», учитывая резко возрастающий с увеличением мощности, а следовательно, и размеров момент инерции ротора.
Если выбрать двигатель с заниженной мощностью, то это может привести к недопустимым рассогласованиям в следящей системе во время «пиковых» нагрузок, отказу в работе и аварии.
Упрощенный выбор мощности двигателя может быть сделан по моменту сопротивления Ме и угловой скорости вала нагрузки ωс в статическом (без ускорений) режиме работы:
![]() (15.13)
(15.13)
где Р-в Вт; Мс-в Н∙м; ωс-рад/с; 1,2-2,5-запас мощности, необходимый для создания ускорений, преодоления максимумов нагрузочного момента и учета КПД редуктора.
1. По найденной мощности Р выбирают двигатель с близким значением мощности.
2. По номинальной
частоте вращения двигателя nном и максимально необходимой угловой
скорости вала нагрузки ωс maxопределяют передаточное отношение редуктора:![]() , где
, где![]()
3. Производят выбор типа редуктора, распределяют общее передаточное отношение редуктора ip по его ступеням и определяют КПД ηр и момент инерции редуктора J'p, приведенный к валу двигателя.
4. По данным двигателя (Jдв), редуктора (ip, ηри J'p нагрузки (Mc и Jc) и заданному среднеквадратичному ускорению вала нагрузки εc ср кв вычисляют эквивалентный момент на валу двигателя:
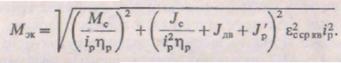
Двигатель выбран правильно, если удовлетворяется неравенство
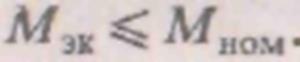
§ 15.9. Выбор двигателя для следящих систем большой мощности
Вследящих системах мощностью до сотен ватт и выше применяют двигатели постоянного тока независимого возбуждения с регулированием угловой скорости по принципу ЭМУ — Д, Г — Д и УВ — Д (см. гл. 4). Особенность таких систем состоит в том, что момент инерции нагрузки, приведенный к валу двигателя, как правило, в несколько раз меньше, чем момент инерции якоря двигателя, а приведенный момент инерции редуктора составляет лишь 5-25% от момента инерции якоря, т. е. при переходных процессах динамический момент двигателя затрачивается в основном на преодоление инерции самого двигателя.
Поскольку приведенные моменты инерции зависят от передаточного отношения редуктора в квадрате, оно является определяющим при выборе двигателя. Для каждого двигателя можно рассчитать оптимальное передаточное отношение редуктора ip opt.
Существует несколько критериев оптимальности ip. Рассмотрим вариант, обеспечивающий приводу максимальное ускорение [15]. Решимуравнение динамики
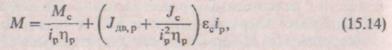
в котором Jдв = (1,05 ÷ 1,25) Jдв-суммарный момент инерциидвигателя с редуктором относительно ускорения вала нагрузки εс. Тогда

Приравняв пулю производную dεc/dip = 0, найдем
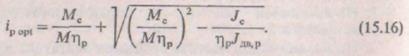
Подставив (15.16) в (15.15), получим максимальное ускорение
![]()
Вычислив по (15.17) Jдв, p и подставив его в (15.14), определим
![]()
Это означает, что система получит максимальное ускорение в том случае, когда на валу нагрузки используется половина вращающего момента М, который развивает двигатель, а вторая половина затрачивается на преодоление момента инерции ротора с редуктором.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.