Исполнительные асинхронные двигатели. Схемы замещения и параметры двухфазных исполнительных асинхронных двигателей. Вращающий момент двухфазного исполнительного асинхронного двигателя. Характеристики исполнительных асинхронных двигателей. Вращающиеся трансформаторы. Универсальные коллекторные двигатели и преобразователи. Синхронные машины общего применения. Синхронные двигатели для систем автоматики, страница 6

а)  механические характеристики: при α = const;

б)  регулировочные характеристики:  или v = f(sin β) при m = const;

в)характеристики мощности управления: при  v = const,

  при α = const;

г)характеристики мощности возбуждения: при  v = const;

при α = const;

 ^д) характеристики полезной (выходной) мощности; при  α = const;

е) зависимость максимальной механической мощности от коэффициента сигнала: при v = const.

На рис. 9.16 приведены механические характеристики исполнительных двигателей при амплитудном (кривая J), фазовом (кривая 2) и амплитудно-фазовом (кривая 3) управлении.

На рис. 9.17 показаны регулировочные характеристики двигателей также при амплитудном (кривая 1), фазовом (кривая 2) и амплитудно-фазовом (кривая 3) управлении.

На рис. 9.18 даны зависимости мощностей управления и возбуждения от частоты вращения при нескольких постоянных значениях коэффициента сигнала. Зависимости мощностей управления и возбуждения от коэффициента сигнала при нескольких постоянных значениях частоты вращения приведены на рис. 9.19. Зависимость полезной механической мощности от частоты вращения при постоянном коэффициенте сигнала представлена на рис. 9.20. На рис. 9.21 дана зависимость максимальной механической мощности от коэффициента сигнала при постоянной номинальной частоте вращения

§ 9.7. Управление двухфазными исполнительными асинхронными двигателями

На рис. 9.22 приведены зависимости вращающего момента исполнительного двигателя от скольжения, определяемые уравнением (9.16). Кривая 1 соответствует активному сопротивлению ротора, при котором критическое скольжение; кривая 2 — активному сопротивлению ротора, при котором

Статическая устойчивость работы двигателя обеспечивается только на участке 0 ≤ s ≤ s_m. Устойчивой работой во всем диапазоне частот вращения 0 ≤ s ≤ 1 обладают только двигатели с характеристикой 2. Регулирование частоты вращения ротора путем изменения напряжения на обмотках статора эффективно только у двигателей с характеристикой 2.

Следовательно, статически устойчивая работа исполнительного двигателя во всем диапазоне частот вращения возможна при s_m≥ 1. Критическое скольжение реальных двигателей s_m = 3 — 4

При амплитудном управлении (рис. 9.23, а) обмотку возбуждения ОВ подключают к сети переменного тока с номинальным напряжением . На обмотку управления ОУ от источника питания ЦП подают сигнал — напряжение управлениясдвинутое по фазе относительно напряжения возбуждения  (напряжения сети) на угол 90°. Управление частотой вращения ротора осуществляют путем изменения амплитудыпри неизменной его фазе (рис. 9.23, б).

Уравнение (9.16) преобразуют к удобному для расчетов виду:

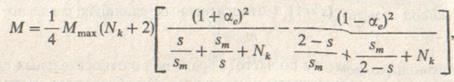 (9.20)

где

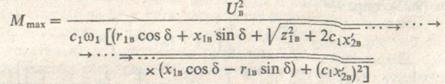 (9.21)

— максимальный момент, соответствующий s_m:  — коэффициент, зависящий от параметров схемы замещения

 — модуль сопротивления обмотки ОВ статора

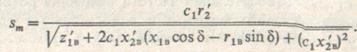   _(9.22)

Входящие в выражения (9.21)-(9.22) модуль с₁ и аргумент δ постоянной с_п для схемы замещения определяются равенствами

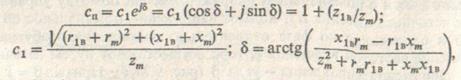
где 

Уравнения (9.17) и (9.18) принимают вид

  (9.23)

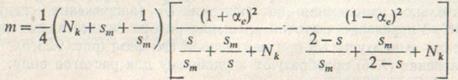 (9.24)

Пусковой момент (s = 1) в относительных единицах согласно (9.24)

                                            (9.25)

Производную момента по частоте вращения в относительных единицах называют коэффициентом внутреннего демпфирования. Используя (9.24) и (9.25), определим