Исполнительные асинхронные двигатели. Схемы замещения и параметры двухфазных исполнительных асинхронных двигателей. Вращающий момент двухфазного исполнительного асинхронного двигателя. Характеристики исполнительных асинхронных двигателей. Вращающиеся трансформаторы. Универсальные коллекторные двигатели и преобразователи. Синхронные машины общего применения. Синхронные двигатели для систем автоматики, страница 5

Такой же вид имеет схема замещения и для напряжения обратной последовательности (рис. 9.15), где составляющая 2-5 показывает, что поле вращается противоположно вращению ротора.

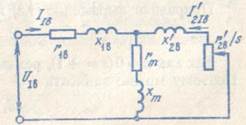
Рис. 9.14. Схема замещения двигателя для напряжений прямой последовательности

Аналогично (9.4) полное сопротивление этой схемы замещения:

                                       (9.5)

где    — полное сопротивление участка схемы замещения

Для расчета емкости пускового конденсатора С_П исходят из условия обеспечения вращающегося поля при включении двигателя. Для определения С_П найдем напряжение обратной последовательности и приравняем его к нулю.

Обозначив через Z_С — сопротивление конденсатора, вычислим

После подстановки (9.7) в (9.6) получим

После преобразований с учетом (9.3) определим

Для упрощения обозначим  Следовательно,

Для обмотки ОУ

Из приведенных выражений получим уравнение для напряжения обратной последовательности:

Поэтому напряжение обратной последовательности

Приравняв выражение (9.8) к нулю, получим

Тaк как n = 0 (s = + 1) режим соответствует короткому замыканию.Поэтому можно записать

где  Кроме того,  Тогда  После несложных преобразований найдем

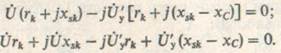
Приравнивая мнимую и вещественную части к нулю  , определим

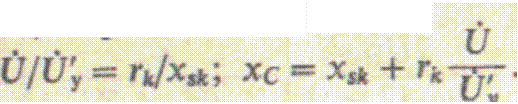                               (9.9)

Считая условие (9.9) выполненным, получим

  (9.10)

   (9.11)

§ 9.5. Вращающий момент двухфазного исполнительного асинхронного двигателя

Используя схемы замещения (рис. 9.14 и 9.15), определим токи в статор-ном и роторном участках исполнительного двигателя, протекающие под действием симметричных составляющих напряжений

  (9.12)

  (9.13)

Модули токов I'_2Iви I'_2IIв прямой и обратной последовательностей в роторе, приведенные к числу фаз статора и числу витков обмотки ОВ, рассчитаем, используя (9.13):

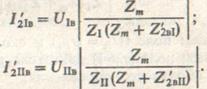  (9.14)

По аналогии с уравнением (8.19) для двухфазного асинхронного двигателя можно записать

  (9.15)

Формула (9.15) справедлива и для нахождения вращающих моментов прямой и обратной последовательностей двигателя. Тогда в соответствии со схемами замещения (рис. 9.14 и 9.15) и выражениями (9.14) уравнения для моментов прямой и обратной последовательностей примут вид

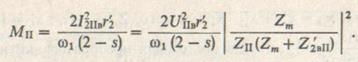
Результирующий момент равен разности моментов прямой и обратной последовательностей:

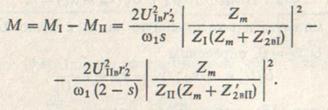  (9.16)

Вращающий момент в относительных единицах рассмотрим относительно пускового момента M_П ,развиваемого двигателем при s = 1 и круговом поле, т. е. при U_Пв = 0, U_Iв = U_в:

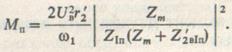  (9.17)

Вращающий момент в относительных единицах равен отношению выражений (9.16) и (9.17)

   (9.18)

Анализируя (9.16), можно сделать следующие выводы:

1) при круговом вращающемся полевращающий момент наибольший:

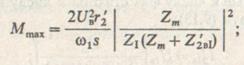   (9.19)

2) при пульсирующем поле и скольжении s = 1 М_п = 0;

3) при пульсирующем поле (s ≠ 1) двигатель развивает вращающий момент прямого или обратного направления;

4) при изменении поля от пульсирующего до вращающегося происходит уменьшение М_ц при одновременном увеличении M_I т. е. результирующий момент растет.

§ 9.6. Характеристики исполнительных асинхронных двигателей

Так же как и для исполнительных двигателей постоянного тока, значения частоты вращения, вращающего момента и напряжения удобнее использовать в относительных единицах:

При  в двигателе имеет место круговое вращающееся поле и эффективный коэффициент сигнала

где — коэффициент трансформации.

С изменением напряжения управления U_yэффективный коэффициент сигнала α_e будет отличным от единицы, а поле — эллиптическим. При  α_e= 0, т. е. снятом сигнале управления, поле становится пульсирующим.

Основными характеристиками двигателей являются;