с = (τком + τизд + τсое + τукл + τобр)Сот + Сзи + Си-об. (V-3)
ПРИЛОЖЕНИЕ VI
Аналитический способ определения экономически оптимального количества производимой продукции
Для аналитического определения экономически оптимального количества производимой продукции Nn.опт необходимо выразить её себестоимость С как функцию от её количества в одной партии Nn. Для этого производится последовательная подстановка формул расчета долей себестоимости продукции (2.3-9), (IV-3) и (V-2) в исходное выражение (2-1)
С(Nn) = ΔСпод(Nn) + ΔСизг(Nn) + ΔСхр(Nn) =
= 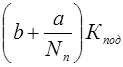 + с +
+ с + 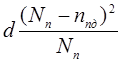 . (VI-1)
. (VI-1)
Преобразования выражения (VI-1)
С(Nn)
= b Кпод + c + ![]() Кпод
+ d
Кпод
+ d 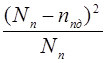 =
=
= b Кпод +
c + ![]() Кпод + d
Кпод + d 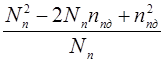 =
=
= b Кпод +
c + ![]() Кпод + d Nn
– 2d nnд + d
Кпод + d Nn
– 2d nnд + d ![]() =
=
= b Кпод +
c – 2d nnд
+ d Nn + ![]() Кпод
+ d
Кпод
+ d ![]() =
=
= (b Кпод +
c – 2d nnд)
+ d Nn + (а Кпод + d ![]() )
)![]() . (VI-2)
. (VI-2)
Оптимальное количество выпускаемой продукции в одной партии, при минимальной её себестоимости, определится из равенства нулю первой производной от функции (VI-2)
С ′(Nn) = 0;
![]() (b Кпод
+ c – 2d nnд)
+ d Nn + (а Кпод + d
(b Кпод
+ c – 2d nnд)
+ d Nn + (а Кпод + d ![]() )
)![]()
![]() =
0. (VI-3)
=
0. (VI-3)
Уравнение (VI-3) включает сумму производных
(b Кпод + c – 2d nnд)′ = 0;
(d Nn)′ = d; (VI-4)
![]() (а Кпод + d
(а Кпод + d ![]() )
)![]()
![]() = – (а Кпод
+ d
= – (а Кпод
+ d ![]() )
)![]() .
.
После подстановки производных (VI-4) в уравнение (VI-3) и его преобразования
d – (а Кпод + d ![]() )
)![]() = 0;
= 0;
(а
Кпод + d ![]() )
)![]() = d;
= d;
а
Кпод + d ![]() = d
= d![]() ;
;
![]() =
= ![]() Кпод
+
Кпод
+ ![]() .
(VI-5)
.
(VI-5)
Из уравнения (VI-5) получаем конечное выражение для определения оптимального количества выпускаемой продукции в одной партии Nn = Nn.опт при её минимальной себестоимости С = Сmin
Nn.опт = 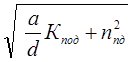 ,
(VI-6)
,
(VI-6)
где параметров а и d входящих в выражение (VI-6) определяются по формулам приведенным в тексте методических рекомендаций.
ПРИЛОЖЕНИЕ VII
Аналитический способ определения экономически
рационального количества производимой продукции
Для определения экономически рационального количества производимой пищевой продукции аналитическим способом используется уравнение получаемое из равенства её себестоимости С(Nn) рыночной цене Ц на эту продукцию (формула (VI-2) приложения VI)
С(Nn) = Ц;
(b Кпод + c – 2d nnд)
+ d Nn + (а Кпод + d ![]() )
)![]() = Ц.
(VII-1)
= Ц.
(VII-1)
Уравнение (VII-1) решается относительно неизвестного параметра, а именно количества продукции Nn в одной партии
d Nn – [Ц – (b Кпод + c – 2d nnд)]
+ (а Кпод + d ![]() )
)![]() = 0;
= 0;
d Nn2 – [Ц
– (b Кпод + c – 2d nnд)] Nn + (а Кпод + d ![]() ) = 0;
) = 0;
Nn2 – 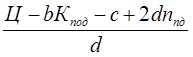 Nn +
Nn + 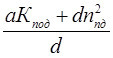 = 0; (VII-2)
= 0; (VII-2)
Полученное выражение (VII-2) является квадратным уравнением
х2 + рх + q = 0, (VII-3)
в котором х = Nn.рац; (VII-4)
р = – 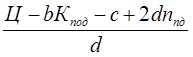 ; (VII-5)
; (VII-5)
q = 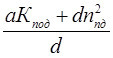 ,
(VII-6)
,
(VII-6)
где параметры а, b, c и d, входящие в выражения (VII-5) и (VII-6) определяются по формулам приведенным в тексте методических рекомендаций.
Корни х1, 2 квадратного уравнения (VII-3) являются границами экономически рациональной области значений количества выпускаемой продукции в одной партии х1, 2 = Nn.рац1,2
х1, 2 = 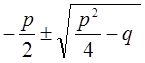 ,
(VII-7)
,
(VII-7)
или при х1, 2 = Nn.рац1,2
Nn.рац1 = 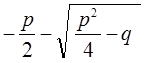 ;
(VII-8)
;
(VII-8)
Nn.рац2 = 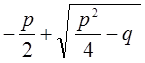 .
(VII-9)
.
(VII-9)
Экономически рациональное количество продукции выпускаемой в одной партии Nп располагается в диапазоне
Nn.рац1 ≤ Nп ≤ Nn.рац2, (VII-10)
|
где |
Nn.рац1 |
- |
нижняя граница экономически рационального количества продукции выпускаемой в одной партии Nп; |
|
Nn.рац2 |
- |
верхняя граница экономически рационального количества продукции выпускаемой в одной партии Nп. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.